salut salut tout le monde , bon voila je suis entrain de bosser un petit test d'analyse et je suis vraiment bloque :mur:
http://www.noelshack.com/2013-01-1388421692-2013-12-30-164041.png
Exercice d'analyse
3 messages
- Page 1 sur 1
Salut,
Bonne année.
-Pour la 2),
Soit . Pose
. Pose  la fonction définie sur [0,1] par:
la fonction définie sur [0,1] par:
 ,
, =f(x)-\lambda g(x))
En remarquant que h est continue (car somme de fonctions continues), le TVI donne de manière immédiate le résultat.
-Pour la 3),
Suppose que pour tout de
de 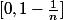 ,
,  ne s'annule pas, alors g est de signe constant (si ce n'était pas le cas, on tomberait sur une contradiction par le TVI).
ne s'annule pas, alors g est de signe constant (si ce n'était pas le cas, on tomberait sur une contradiction par le TVI).
On peut supposer que est strictement positive (le cas strictement négative est analogue)
est strictement positive (le cas strictement négative est analogue)
Alors on a pour tout de
de 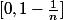 ,
, >f(x))
Donc en appliquant successivement à cette inégalité les valeurs ,
,  ,...,
,...,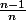 on a :
on a :
<f(\frac{0+1}{n})<f(\frac{1+1}{n})<\cdots\, <f(\frac{n-2+1}{n})<f(\frac{n-1+1}{n})=f(1)) ,
,
Puis tu obtiens une contradiction
(on pouvait aussi procéder par des récurrences pour que ce soit plus élégant)
-Pour la 4)
 est prolongeable par continuité en un certain point si et seulement si elle a une limite finie en ce point.
est prolongeable par continuité en un certain point si et seulement si elle a une limite finie en ce point.
(je te laisse les calculs, mais en tu devrais trouver que en 0 c'est oui, et en 1 c'est non)
Bonne année.
-Pour la 2),
Soit
En remarquant que h est continue (car somme de fonctions continues), le TVI donne de manière immédiate le résultat.
-Pour la 3),
Suppose que pour tout
On peut supposer que
Alors on a pour tout
Donc en appliquant successivement à cette inégalité les valeurs
Puis tu obtiens une contradiction
(on pouvait aussi procéder par des récurrences pour que ce soit plus élégant)
-Pour la 4)
(je te laisse les calculs, mais en tu devrais trouver que en 0 c'est oui, et en 1 c'est non)
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
