Analyse

[C.l]

Bonjour,

je ne comprend pas vraiment bien les sommes, par exemple que signifie cela:

(n+1)^p = Somme allant de k=0 à n de k^p


Merci a vous!

[Ericovitchi]

Tout dépend ce que tu ne comprends pas ?
tu comprends ?
ça veut dire

Après, aucune raison que ça vaille :hein:
(essaye par exemple p=2 et n=2, 1²+2² vaut 5 et 3² vaut 9 donc ça n'est pas égal)

Donc quelle est exactement ta question ?

[kamsar]

Résoudre l'équation dans C
Z^4-(8i+8)Z^3+48iZ^2-64(i-1)Z-80=0
Sachant qu'elle admet une racine réelle Z0 et une racine imaginaire pure Z1

[Ben314]

Posons (pour gagner du temps)
Si est un réel (et uniquement dans ce cas là), alors 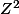, 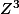et sont des réels donc la partie réelle de est :
et la partie imaginaire de est :

De plus, pour que soit nul, il faut que ces deux quantitées là soient toutes les deux nulles.
On peut donc (par exemple), résoudre l'équation puis regarder la(les)quelles des solutions marchent aussi dans l'équation

A priori, vu qu'on ne sait résoudre que les équations de degré 2 et que celle de départ est de degré 4, on peut espérer trouver 2 solutions par cette méthode si celui qui a posé l'exercice est "gentil'.


P.S. Si je te dit "le Parioux", ça évoque quelque chose ?

[C.l]

Tout dépend ce que tu ne comprends pas ?
tu comprends ?
ça veut dire

Après, aucune raison que ça vaille :hein:
(essaye par exemple p=2 et n=2, 1²+2² vaut 5 et 3² vaut 9 donc ça n'est pas égal)

Donc quelle est exactement ta question ?

enfaite la formule du binome de newton je ne lai pas compris avec les n parmis les k...

[Sylviel]

La formule de Newton est à connaître par coeur. Elle peut néanmoins se comprendre assez naturellement :

(a+b)^3 = (a+b)(a+b)(a+b) = aaa+ aab + aba + abb + baa+ bab + bba + bbb

On obtient une grosse somme où, pour chaque termes, je choisis a ou b.

Combien donnerons b^3 ? Une seule : il faut prendre les b à chaque fois.
Combien donnerons a b^2 ? 1 parmi 3, car je choisis 1 parenthèses parmis les 3 où je prends a et le reste c'est b
Combien donnerons a^2 b ? 2 parmi 3, car je choisis 2 parenthèses parmis les 3 où je prends a et le reste c'est b

De manière plus générale pour (a+b)^n, le terme qui contient k fois a contiendras logiquement n-k fois b, et il apparaît k parmis n fois dans ma grosse somme. En effet je choisis k parenthèses parmis n qui me donnerons a, les autres me donnant b.

[Ericovitchi]

Ha alors c'est
que tu as cherché à écrire ?

[alavacommejetepousse]

La formule de Newton est à connaître par coeur

Bonjour
je précise :
seulement pour ceux qui font un peu de mathématiques.

[C.l]

Ha alors c'est
que tu as cherché à écrire ?

Oui c'est exactement ça....

[Ericovitchi]

Et bien tu étais vraiment loin du compte. Somme allant de k=0 à n de k^p n'a pas grand chose à voir avec l'expression que j'ai écrite.