Exercice suites

par **Anonyme** » 25 Déc 2013, 12:00

Bonjour ce serait très gentil de votre part de m'aider dans un exercice sur le suites merci par avance :lol3:

La suite Un est définie par

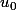
=0 et pour tout entier naturel n;

=

1/ Calculer

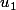
et

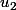
. ça c'est bon j'ai trouvé

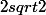
et

2/ Démontrer par récurence que pour tout n de N: 0

. celle la je n'y arrive pas du tout.
3/ a. Justifier que cette suite est convergente
b. En remarquant que pour tout n de N:

montrer que la limite L de la suite vérifie une équation et en déduire la valeur de cette limite.
4/On se propose d'obtenir l'expression de cette suite en fonction de n.
a. La suite

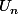
est définie sur N par

. Démontrer que la suite

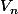
est géométrique.
b. En déduire l'expression de

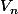
puis de

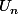
en fonction de n.
c. Retrouver alors la limite de

.

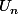
merci par avance de votre généreuse aide :we:

par **Anonyme** » 25 Déc 2013, 12:18

la1/ c'est bon
la 2/ non
la 3/ a. non
b. c'est bon
la 4/ a. c'est Vn géométrique de raison 0.5 et de premier terme V0=-16
b.c'est bon

et

c. non

par **Anonyme** » 25 Déc 2013, 13:57

<3boubou<3 a écrit:la1/ c'est bon
la 2/ non
la 3/ a. non
b. c'est bon
la 4/ a. c'est Vn géométrique de raison 0.5 et de premier terme V0=-16
b.c'est bon et
c. non

personne??

par **JaafarSecure** » 25 Déc 2013, 14:38

Pour la 2/ tu la découpe en 2 .. tu démontre en premier par récurrence que Un+1-Un est plus grande que0 apres tu passes à la deuxième partie

par **JaafarSecure** » 25 Déc 2013, 14:41

Pour la 3/a .. D'après la question précédente tu as résolu que Un+1 -Un est plus grande que zero ce qui fait .. et tu sais bien que UN est plus petite que 8 donc.. et pour la 3/2 tu crées une fonction (Un+1=f(Un))

par **jaimemaths** » 25 Déc 2013, 21:03

Pout 2/ tu dois procéder comme suit

On suppose que

Et on montre

Allons-y

Nos avons supposé que

donc on met tout au carré

Après on multiplie par 0,5 (0,5 > 0) et on ajoute 8

On prend le racine de tout car la fonction racine de x est croissante

Donc

CQFD

J'espère que je n'ai pas fait d'erreur :lol3:

par **jaimemaths** » 25 Déc 2013, 21:21

Pour 3/ a) tu vois que que d'après 2) la suite est croissante et est minorée donc converge vers

tel que:

3/ b) tu calcul cette limite car

et tu cherchera

avec l'équation suivante

Bonne chance :lol3:

par **jaimemaths** » 25 Déc 2013, 21:31

Tu verra le 4/ b) je pense que c faux.

puisque

est géométrique de raison

alors on peut écrire

Tu trouvera alors

en fonction de

:lol3:

par **Anonyme** » 26 Déc 2013, 11:32

jaimemaths a écrit:Pour 3/ a) tu vois que que d'après 2) la suite est croissante et est minorée donc converge vers tel que:

3/ b) tu calcul cette limite car

et tu cherchera avec l'équation suivante

Bonne chance :lol3:

merci c'est très gentil de m'avoir répondu
Oui pour la 3.b j'ai trouvé aussi L²=0.5L²+8 Donc L=4

par **Anonyme** » 26 Déc 2013, 11:42

jaimemaths a écrit:Tu verra le 4/ b) je pense que c faux.

puisque est géométrique de raison alors on peut écrire

Tu trouvera alors en fonction de

:lol3:

moi pour cette question j'ai fait:

Et comme,

Donc

par **Anonyme** » 26 Déc 2013, 11:44

<3boubou<3 a écrit:moi pour cette question j'ai fait:

Et comme,

Donc

Attention les +1 sont tous en puissances avec le n c'est 0.5 puissance n+1 je n'ai pas réussi à les mettre tous les deux ensemble :hum:

par **jaimemaths** » 26 Déc 2013, 14:47

Salut,

Tu ne peux pas faire ça car on ne te demande pas de chercher la somme des

alors refaits ce que je t'ai écrit en haut pour

en fonction de

:we:

par **Tiruxa** » 26 Déc 2013, 15:34

Bonjour

Ne pas chercher de complications, utiliser la définition explicite (c'est à dire en fonction de n) d'une suite

de premier terme -16 et de raison 0,5.

C'est le tout début de la leçon

par **Anonyme** » 26 Déc 2013, 17:18

jaimemaths a écrit:Salut,

Tu ne peux pas faire ça car on ne te demande pas de chercher la somme des

alors refaits ce que je t'ai écrit en haut pour en fonction de

:we:

désolé mais je comprends pas ce que vous voulez dire je ne vois où on me demande de chercher la somme :hein:

par **Anonyme** » 26 Déc 2013, 17:25

Tiruxa a écrit:Bonjour

Ne pas chercher de complications, utiliser la définition explicite (c'est à dire en fonction de n) d'une suite de premier terme -16 et de raison 0,5.

C'est le tout début de la leçon

C'est çà??? :hein:

par **Anonyme** » 26 Déc 2013, 18:18

<3boubou<3 a écrit:
C'est çà??? :hein:

Quelqu'un s'il vous plaît je l'ai bientôt fini :cry:

par **Tiruxa** » 26 Déc 2013, 19:45

oui c'est ça en effet

par **Anonyme** » 26 Déc 2013, 22:21

Tiruxa a écrit:oui c'est ça en effet

ok merci :lol3:

donc

mais après je ne sais pas comment faire c'est la dernière question :hum:

par **Tiruxa** » 27 Déc 2013, 01:04

<3boubou<3 a écrit:ok merci :lol3:

donc
mais après je ne sais pas comment faire c'est la dernière question :hum:

Chercher la limite de

comme suite géométrique dont la raiso 0,5 est strictement comprise entre 0 et 1 (voir cours)

En déduire ensuite celle de

Exercice suites

Exercice suites

Qui est en ligne