DM Suites T°S

par **wakaloup35** » 07 Nov 2013, 19:06

Bonjour bonsoir,

J'ai un DM à faire sur les suites, je n'arrive pas à définir la propriété Pn pour commencer, ni à comprendre le reste d'ailleurs. Voici l'énoncé :

On considère la suite (Un) définie par [1;3] et pour tout N,
1- L'intervalle I = [1;3] semble contenir tous les termes de la suite. Démontrez par récurrence que tous les termes (U_n) appartiennent à I.

2- Conjecturez le sens de variation de la suite () puis démontrez votre conjecture.

3- Démontrez que la suite () est convergente et conjecturez sa limite.

Merci pour votre aide

par **t.itou29** » 07 Nov 2013, 20:11

Salut !
Pour montrer que pour tout n,

tu dois montrer que:

, et il s'agit de ta propriété Pn à montrer

par **wakaloup35** » 07 Nov 2013, 21:01

pour hérédité, je trouve à la fin :

Et comme cet intervalle appartient à I et que

alors 1

3

J'ai l'impression d'avoir fait n'importe quoi cependant

par **wakaloup35** » 07 Nov 2013, 21:18

pour la question 2, ma conjecture : Un est strictement croissante. Comment je peux le démontrer ?
Parce que on sait juste que Un est compris dans [1;3] je fais comment sans son expression pour dire que Un+1>= à Un ?

par **chombier** » 07 Nov 2013, 21:36

wakaloup35 a écrit:pour la question 2, ma conjecture : Un est strictement croissante. Comment je peux le démontrer ?
Parce que on sait juste que Un est compris dans [1;3] je fais comment sans son expression pour dire que Un+1>= à Un ?

Cherche le signe de

.

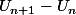
Il faudra peut-être utiliser l'expression conjuguée (l'expression conjuguée à

est

)

par **wakaloup35** » 08 Nov 2013, 07:58

Bah c'est positif mais ça sert à quoi ?

par **t.itou29** » 08 Nov 2013, 16:35

wakaloup35 a écrit:Bah c'est positif mais ça sert à quoi ?

Si c'est positif c'est que Un+1>Un, donc que ?

DM Suites T°S

DM Suites T°S

Qui est en ligne