équation trigono
19 messages
- Page 1 sur 1
équation trigono
Bonjour, est-ce que quelqu'un pourrait m'aider à résoudre cette équation :
2cos^2(2x)=sin^2(4x)
merci d'avance
2cos^2(2x)=sin^2(4x)
merci d'avance
Bonjour,
une première idée pour y voir plus clair :
poser X=2x.
Ton équation sera un peu plus simple.
Ensuite il faut faire un choix : soit avoir des angles différents, soit avoir des puissances différentes. Ici je te conseille de commencer par te ramener à des sin(X) et cos(X) (à la puissance adéquate). Ensuite tu verras bien !
P.S: en trigo plus qu'ailleurs il faut faire plein d'essais. Connaître les formules est un prérequis nécessaire mais loin d'être suffisant !
une première idée pour y voir plus clair :
poser X=2x.
Ton équation sera un peu plus simple.
Ensuite il faut faire un choix : soit avoir des angles différents, soit avoir des puissances différentes. Ici je te conseille de commencer par te ramener à des sin(X) et cos(X) (à la puissance adéquate). Ensuite tu verras bien !
P.S: en trigo plus qu'ailleurs il faut faire plein d'essais. Connaître les formules est un prérequis nécessaire mais loin d'être suffisant !
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Sylviel a écrit:Bonjour,
une première idée pour y voir plus clair :
poser X=2x.
Ton équation sera un peu plus simple.
Ensuite il faut faire un choix : soit avoir des angles différents, soit avoir des puissances différentes. Ici je te conseille de commencer par te ramener à des sin(X) et cos(X) (à la puissance adéquate). Ensuite tu verras bien !
P.S: en trigo plus qu'ailleurs il faut faire plein d'essais. Connaître les formules est un prérequis nécessaire mais loin d'être suffisant !
Merci pour cette réponse
fant4, c'est bien, tu suis les étapes que l'on te donne. Mais il faut faire plus, il faut essayer de les utiliser sur ton équation sans que l'on te guide à chaque moment. Après l'indication sin(2x)=... tu aurais pu cherche à voir comment l'utiliser. Ou alors tu aurais pu prendre mon indication de faire un changement de variable pour y voir plus clair.
Maintenant on t'indique que tu peux l'utiliser pour sin(4x), donc essaie de l'utiliser dans ton équation pour voir où cela te mène...
Maintenant on t'indique que tu peux l'utiliser pour sin(4x), donc essaie de l'utiliser dans ton équation pour voir où cela te mène...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Sylviel a écrit:fant4, c'est bien, tu suis les étapes que l'on te donne. Mais il faut faire plus, il faut essayer de les utiliser sur ton équation sans que l'on te guide à chaque moment. Après l'indication sin(2x)=... tu aurais pu cherche à voir comment l'utiliser. Ou alors tu aurais pu prendre mon indication de faire un changement de variable pour y voir plus clair.
Maintenant on t'indique que tu peux l'utiliser pour sin(4x), donc essaie de l'utiliser dans ton équation pour voir où cela te mène...
Bonjour,
je suis finalement arrivé à ce résonnement.
Est-il bon ?
Il me semble que je n'ai pas trouvé toutes les valeurs possibles ?
2cos^2(2x) = sin^2(4x)
2cos^2(2x) = (2sin(2x)*cos(2x))^2
(cos(2x)*sqrt(2))^2 = (2sin(2x)*cos(2x))^2
cos(2x)*sqrt(2) = 2sin(2x)*cos(2x)
cos(2x) = sqrt(2)sin(2x)*cos(2x)
1 = sqrt(2)sin(2x)
sqrt(2)/2 = sin(2x)
(k est un naturel)
2x = pi()/4 + k2pi()
x = pi()/8 + k*pi()
2x = pi() - pi()/4 + k2pi()
x = pi()/2 - pi()/8 + k*pi()
x = 3pi()/8 + k*pi()
2x = -pi()/4 + k2pi()
x = -pi()/8 + k*pi()
2x = pi() + pi()/4 + k2pi()
x = 5pi()/8 + k*pi()
Salut !
J'aurai raisonner ainsi :
Posons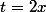 , résolvons alors
, résolvons alors =sin^2 (2t)) .
.
=2\sin(t)\cos(t)) , on a
, on a =4\sin^2 (t) \cos^2 (t)) .
.
Cela équivaut donc à ( 1-2\sin^2 (t) ) =0) .
.
En conséquence,=0) ou
ou  =0) .
.
Or =0) équivaut à
équivaut à  - \frac{\sqrt 2 }{2 }\) \( \sin(t) + \frac{\sqrt 2 }{2 }\) =0) .
.
Donc en conclusion,=0) OU
OU  - \frac{\sqrt 2 }{2 }=0) OU
OU  + \frac{\sqrt 2 }{2 }=0) .
.
Je te laisse finir quant à l'ensemble des solutions :+++:
J'aurai raisonner ainsi :
Posons
Cela équivaut donc à
En conséquence,
Or
Donc en conclusion,
Je te laisse finir quant à l'ensemble des solutions :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
