Ensembles et applications

[Vanette]

Image directe et image réciproque

Bonjour,je n'arrive pas à terminer l'exercice, bloquée à partir de la question :mur: 1b (voir liens):

Enoncé+question 1

Questions 2 et 3

Merci d'avance :happy2:

[Vanette]

Pour 1b
Disons que je sais que :
-f surjective s'écrit quelque soit y appartenant à F il existe x appartenant à E tel que f(x)=y
-;) surjective s'écrit quelque soit B appartenant à P(F) il existe A appartenant à P(E) tel que f(A)=B (égalité d'ensemble)

dans le sens =>
j'ai supposé f surjective
Soit B ;)P(F) et y ;) B
f surjective donc il existe x appartenant à A tel que f(x)=y
or (def de l'image direct) si x ;) A, f(x) ;) f(A) donc y ;) f(A)
donc B inclus dans F(A)

après je ne sais pas montrer l'autre inclusion et l'autre implication non plus.

[mrif]

Pour 1b
Disons que je sais que :
-f surjective s'écrit quelque soit y appartenant à F il existe x appartenant à E tel que f(x)=y
-;) surjective s'écrit quelque soit B appartenant à P(F) il existe A appartenant à P(E) tel que f(A)=B (égalité d'ensemble)

dans le sens =>
j'ai supposé f surjective
Soit B P(F) et y B
f surjective donc il existe x appartenant à A tel que f(x)=y
or (def de l'image direct) si x A, f(x) f(A) donc y f(A)
donc B inclus dans F(A)

après je ne sais pas montrer l'autre inclusion et l'autre implication non plus.

Pour l'autre sens, soit y appartenant à F, la partie {y} a un antécédent par "grand phi". Un élément de cet antécédent est un antécédent de y pour f, donc f est surjective.

[Vanette]

D'accord, ça c'est bon merci. :happy2:
Pour l'autre implication, une idée ? j'étais sur la bonne voie ou pas du tout ?

[mrif]

D'accord, ça c'est bon merci. :happy2:
Pour l'autre implication, une idée ? j'étais sur la bonne voie ou pas du tout ?

Ta réponse n'est pas correcte.

Pour simplifier l'écriture, je renomme le "grand phi" par H.
Soit B un élément de P(F), on cherche A tel que H(A) = B.

On sait que f(A) est inclus dans B
Soit y appartenant à B. Puisque f est surjective, il existe x dans E tel que f(x) = y
Par définition de A, x appartient à A, donc y = f(x) appartient à B ce qui montre que B est inclus dans f(A). La double inclusion montre que f(A) = B donc H est surjective.

[Vanette]

Ta réponse n'est pas correcte.

Pour simplifier l'écriture, je renomme le "grand phi" par H.
Soit B un élément de P(F), on cherche A tel que H(A) = B.

On sait que f(A) est inclus dans B
Soit y appartenant à B. Puisque f est surjective, il existe x dans E tel que f(x) = y
Par définition de A, x appartient à A, donc y = f(x) appartient à B ce qui montre que B est inclus dans f(A). La double inclusion montre que f(A) = B donc H est surjective.

d'accord j'ai compris merci beaucoup

[Vanette]

Re (Salut)

J'en suis à la 2a et b
J'ai du mal quand surjectif et injectif se mélange et je n'ai jamais su démontré par l'absurde quelqu'un à une indication ?

je suppose f non injective (donc il existe (x1,x2) appartenant à E^2 tel que f(x1)=f(x2) et x1 différent de x2)
et ;) surjective (donc il existe B appartenant à P(F) tel que f^-1=A)

mais je ne vois pas comment arriver à la contradiction :triste:

même problème dans l'autre sens

(je suppose f injective (donc quelque soit (x1,x2) appartenant à E^2 tel que f(x1)=f(x2) => x1=x2)
et ;) non surjective (donc il existe A appartenant à P(E) tel que quelque soit B appartenant à P(F) tel que f^-1 différent de A))

[Ben314]

Je ne suis pas certain qu'un raisonnement par l'absurde soit indispensable.

Pour le 1), dans le sens =>, tu suppose f injective et il faut montrer que est surjective.
On prend donc un A de l'ensemble d'arrivé de , c'est à dire P(E) et on doit trouver un B de l'ensemble de départ P(F) de , tel que .
Comment construire une partie de F partant d'une partie de E ?
Vu le contexte, il semble qu'il n'y ait pas trop le choix : on prend pour B l'image directe de A par f, c'est à dire .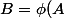
Il reste à montrer que , c'est à dire est en fait égal à A (par double inclusion vu que ce sont des ensembles et en n'oubliant pas qu'on va surement utiliser quelque part le fait que f est injective)