Exercice sur les distribtions

[Supernova]

Hello forum!

Je suis là pour demander de l'aide concernant un exercice portant sur le chapitre des distributions dont voici l'énoncé:

soit U une distribution telle que xU=0
soit une fonction de D(IR) qui ne s'annule pas en 0. Montrer qu'il existe une constante , pour toute fonction qui vaut 1 sur le support de on a:

J'ai essayé de trouver la solution mais malheureusement je n'ai abouti à rien, donc s'il vous plaît est-ce que vous pouvez me donner un coup de main.

Merci d'avance

[L.A.]

Bonjour.

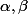
Il s'agit que montrer que si sont deux fonctions-test qui valent 1 sur le support de , alors .

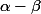
Que peux-tu dire des points où la fonction test s'annule ?

[Supernova]

Bonjour.

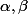
Il s'agit que montrer que si sont deux fonctions-test qui valent 1 sur le support de , alors .

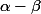
Que peux-tu dire des points où la fonction test s'annule ?

Ce sont des points du support de phi

[L.A.]

Ce sont des points du support de phi

Ce sont tous les points du support de phi et d'autres éventuellement.
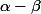
Tu sais donc que s'annule en 0 (et même sur un voisinage de 0)
Qu'est-ce que tu peux en déduire sur le lien entre cette fonction et la fonction x ? (en utilisant une formule de Taylor par exemple)

[Supernova]

Ce sont tous les points du support de phi et d'autres éventuellement.
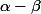
Tu sais donc que s'annule en 0 (et même sur un voisinage de 0)
Qu'est-ce que tu peux en déduire sur le lien entre cette fonction et la fonction x ? (en utilisant une formule de Taylor par exemple)

on peut écrire alors: où est continue et tq
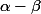
Donc en appliquant U à on trouve que c'est égal à zéro et c'est le résultat qu'on cherche n'est-ce pas?

[L.A.]

Oui, il suffit juste de vérifier que psi est bien une fonction-test (c'est à dire C^infini a support compact) et ça marche (je ne vois pas à quoi sert ta majoration par contre)