Somme et trigonométrie !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bbop
- Messages: 8
- Enregistré le: 28 Oct 2013, 15:38
-
 par bbop » 28 Oct 2013, 15:50
par bbop » 28 Oct 2013, 15:50
Bonjour à tous ! Je suis bloquée à un petit exercice de math et ça m'embête vraiment de pas trouver :mur:
Je vous donne l'énoncé :
Soit

1. La premiere question demande d'exprimer
-tan(b))
sous un quotient et j'obtient :
-tan(b)=sin(a-b)/(cos(a)cos(b)))
2. On nous demande d'en déduire en fonction de x une autyre expression pour
cos((k+1)x)))
Et la je coince.. Car en prenant a=kx et b=(k+1)x,
-tan((k+1)x)=sin(-x)/(cos(kx)cos((K+1)x)))
Et comme x ne peut pas valoir un multiple de pi/2.. Je coince !
Merci !
-
Black Jack
 par Black Jack » 28 Oct 2013, 16:38
par Black Jack » 28 Oct 2013, 16:38
avec a = (k+1)x et b = kx :
tan((k+1)x) - tan(kx) = sin(x)/(cos(kx).cos((k+1)x))
1/(cos(kx).cos((k+1)x)) = (tan((k+1)x) - tan(kx))/sin(x)
Et c'est uniquement valable si x n'est multiple de Pi/2 ... car on ne peut pas diviser par 0 (dans le membre de gauche) et dans le memebre de droite, (tan((k+1)x) - tan(kx)) n'est pas non plus définie pour x = multiple de Pi/2.
Qu'est ce qui t'interpelle là dedans ?
:zen:
-
bbop
- Messages: 8
- Enregistré le: 28 Oct 2013, 15:38
-
 par bbop » 28 Oct 2013, 16:58
par bbop » 28 Oct 2013, 16:58
Mais oui je suis trop bête sérieux.. Quelle méga quiche :langue:
Et dans la dernière question, il demande de calculer la somme de k=1 à n de 1/(cos(kx).cos((k+1)x))
Je trouve
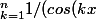cos((k+1)x))= 1/sin(x)*(\bigsum_{k=1}^{n} tan(kx+x) - \bigsum_{k=1}^{n} tan(kx)))
C"'est bien ça ? Parce contre je ne vois pas vraiment comment aller plus loin dans le calcul..
-
Black Jack
 par Black Jack » 29 Oct 2013, 10:20
par Black Jack » 29 Oct 2013, 10:20
bbop a écrit:Mais oui je suis trop bête sérieux.. Quelle méga quiche :langue:
Et dans la dernière question, il demande de calculer la somme de k=1 à n de 1/(cos(kx).cos((k+1)x))
Je trouve
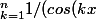cos((k+1)x))= 1/sin(x)*(\bigsum_{k=1}^{n} tan(kx+x) - \bigsum_{k=1}^{n} tan(kx)))
C"'est bien ça ? Parce contre je ne vois pas vraiment comment aller plus loin dans le calcul..
Somme (de k = 1 à n) de [tan((k+1)x) - tan(kx)] = (tan(
2x) - tan(x)) + (tan(
3x) - tan(
2x)) + (tan(4x) - tan(
3x)) + ... + (tan((n+1)x) - tan(nx))
Et on voit que dans le 2ème membre, presque tous les termes se simplifient (sauf 2) et donc ...
:zen:
 par busard_des_roseaux » 29 Oct 2013, 10:54
par busard_des_roseaux » 29 Oct 2013, 10:54
Et dans la dernière question, il demande de calculer la somme de k=1 à n de 1/(cos(kx).cos((k+1)x))
Je trouve
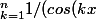cos((k+1)x))= 1/sin(x)*(\bigsum_{k=2}^{n+1} tan(kx) - \bigsum_{k=1}^{n} tan(kx)))
car
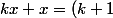x)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités