Nombres complexes

[GeorgiaDzit]

Bonjour j'ai reçu un dm,et le premier exercice me laisse perplexe,je suis perdu quand je commence un calcule pourriez vous m'aider s'il vous plait,merci , je vous l’énnonce!

Soient les nombres complexes : z1 = 1- i racine de 3 et z2 = 1/racine de 3 + 1/3 i

Calculer sous forme algèbrique : a) z1 + z2
b) complément de z1 - z2
c) z1*z2
d) 1/z1

[LeFish]

Si on note et deux nombres complexes, alors


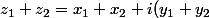Normalement dans ton cours il devrait y avoir la définition du complément !

Pour le produit, il suffit de développer ton expression.

Pour l'inverse de z1, utilise la quantité conjuguée (dis-moi si tu ne sais pas du tout ce que c'est et que ce n'est pas dans ton cours)

[GeorgiaDzit]

Si on note et deux nombres complexes, alors


Normalement dans ton cours il devrait y avoir la définition du complément !

Pour le produit, il suffit de développer ton expression.

Pour l'inverse de z1, utilise la quantité conjuguée (dis-moi si tu ne sais pas du tout ce que c'est et que ce n'est pas dans ton cours)

Je n'ai plus mon cours,je l'avais en première ,et maintenant je suis en terminale,c'est pour ça que je n'y arrive pas

[LeFish]

Du coup la somme tu peux faire.

Pour la suite tu calcules z1 - z2 comme pour la somme (sauf que dans ma formule ça devient x1 - x2 + i(y1 - y2).

Pour le produit, tu développes l'expression sachant que i²=-1.

Pour l'inverse de z1, tu multiplies numérateur et dénominateur par le conjuguée de z1, qui est x1 - i y1 (si je reprends mes notations du début)

Remarque au passage : normalement si tu es passé en terminale c'est que tu es censé connaître le programme de première. Bosse plus donc !

[GeorgiaDzit]

Je peux vous montrez ce qu'on m'a commencé pour le a) ?

[LeFish]

Recopie ce que tu as et je verrai ;)

[GeorgiaDzit]

z1 + z2
= (1-iV3) + ( 1/V3 + 1/3 i)
= 1 - iV3 + 1/V3 + 1/3.i
= 4 + i(-V3 + 1/3)
= 4 + i(-3V3/3 + 1/3)
= 4 + i ((1-3V3)/3)

mais ça me paraissait complexe donc je préfère demander

[LeFish]

Il y a une erreur, normalement on ne doit pas trouver 4 mais , qu'on ne peut pas trop simplifier.

[GeorgiaDzit]

Donc je remplace 4 par ce que vous avez dit, et le reste est bon ou pas ?

[LeFish]

Yes!
Ecrire 4 ça revient à dire que , ce qui est un peu bizarre.

[GeorgiaDzit]

Sinon après mon calcul est finis ou je dois encore développé la partie entre parenthèse ?

[LeFish]

Nonon, c'est bon. Concentre-toi sur la suite des exos plutôt ;)

[GeorgiaDzit]

Nonon, c'est bon. Concentre-toi sur la suite des exos plutôt

J'ai fait la e)

1/z1
=1* 1-iV3 / (1-iV3)(1-iV3)
=1-iV3 / -2


??

[LeFish]

Comment tu fais exactement pour passer de la 2e à la 3e ligne ?
Tu n'as pas multiplié numérateur et dénominateur par la bonne quantité...

[GeorgiaDzit]

Comment tu fais exactement pour passer de la 2e à la 3e ligne ?
Tu n'as pas multiplié numérateur et dénominateur par la bonne quantité...

Le dénominateur j'ai developpé

J'ai multiplié avec laquelle alors ?

[LeFish]

Tu as multiplié avec la mauvaise !
Quand je dis de multiplier par la quantité conjuguée, le conjugué d'un nombre complexe c'est si le nombre complexe auquel on s'intéresse est .
Dans ton cas, quel est le conjugué de ?

Et aussi : est-ce que tu penses que est égal à -2 ?

[GeorgiaDzit]

Tu as multiplié avec la mauvaise !
Quand je dis de multiplier par la quantité conjuguée, le conjugué d'un nombre complexe c'est si le nombre complexe auquel on s'intéresse est .
Dans ton cas, quel est le conjugué de ?

Et aussi : est-ce que tu penses que est égal à -2 ?

C'est z1 = x1 + i y1 le conjugué (ou un - à la place du +) ?

Et non je me suis trompé dans le développement !

[LeFish]

C'est un -.
Si tu préfères, prendre le conjugué d'un nombre complexe c'est changer le signe qui est juste devant le "i".

[GeorgiaDzit]

Ah d'accord!
Mais c'est avec celui la que j'ai calculé pourtant...

[LeFish]

Tu n'as pas compris ! (Mais il est possible que j'ai mal expliqué.)

Le conjugué de c'est , donc c'est avec Cette quantitué que tu dois multiplier numérateur et dénominateur !