Problème Etude de fonctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Toxik
- Membre Naturel
- Messages: 23
- Enregistré le: 30 Aoû 2013, 18:43
-
 par Toxik » 30 Aoû 2013, 18:50
par Toxik » 30 Aoû 2013, 18:50
Salut, je viens ici en dernier recourt car je m'arrache les cheveux sur le dm que mon prof m'a donné.
Voila l'exercice :
On considère la fonction f définie par
=\frac{x-3}{x^2+x+4})
On note Cf la courbe représentative de f dans un repère orthogonal (O;i;j)
Unités: 1 cm pour 1 en abscisses et 10 cm pour 1 en ordonnées.
1.Justifier que f est définie sur R
2.Calculer f'(x) et en déduire les variations de f sur R
3.Déterminer l'équation de la tangente T de Cf au point d'abscisses 2.
4.Tracer T et Cf.
Merci de vos réponses
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Aoû 2013, 19:16
par Carpate » 30 Aoû 2013, 19:16
Toxik a écrit:Salut, je viens ici en dernier recourt car je m'arrache les cheveux sur le dm que mon prof m'a donné.
Voila l'exercice :
On considère la fonction f définie par
=\frac{x-3}{x^2+x+4})
On note Cf la courbe représentative de f dans un repère orthogonal (O;i;j)
Unités: 1 cm pour 1 en abscisses et 10 cm pour 1 en ordonnées.
1.Justifier que f est définie sur R
2.Calculer f'(x) et en déduire les variations de f sur R
3.Déterminer l'équation de la tangente T de Cf au point d'abscisses 2.
4.Tracer T et Cf.
Merci de vos réponses
Bonsoir,
je ne vois dans ce problème qu'une application immédiate d'un cours sur l'étude des fonctions.
Qu'est-ce qui te bloque ?
Pour quelle éventuelles valeurs de x f serait-elle non définie ?
-
Toxik
- Membre Naturel
- Messages: 23
- Enregistré le: 30 Aoû 2013, 18:43
-
 par Toxik » 30 Aoû 2013, 20:14
par Toxik » 30 Aoû 2013, 20:14
Carpate a écrit:Bonsoir,
je ne vois dans ce problème qu'une application immédiate d'un cours sur l'étude des fonctions.
Qu'est-ce qui te bloque ?
Pour quelle éventuelles valeurs de x f serait-elle non définie ?
Je n'arrive pas à la question 2, je trouve
=\frac{-x^2+6x+1}{(x^2+x+4)^2})
Déjà je ne suis pas sur de ce résultat et je n'arrive pas à déduire la variation de f

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 30 Aoû 2013, 21:28
par Ericovitchi » 30 Aoû 2013, 21:28
Petite erreur dans la dérivée
=\dfrac{-x^2+6x+7}{(x^2+x+4)^2)
il te reste à étudier son signe. Elle est du signe du numérateur donc d'un polynôme du second degré (Rappel : il est du signe de a à lextérieur de ses racines s'il en a)
-
Toxik
- Membre Naturel
- Messages: 23
- Enregistré le: 30 Aoû 2013, 18:43
-
 par Toxik » 30 Aoû 2013, 22:30
par Toxik » 30 Aoû 2013, 22:30
Ericovitchi a écrit:Petite erreur dans la dérivée
=\dfrac{-x^2+6x+7}{(x^2+x+4)^2)
il te reste à étudier son signe. Elle est du signe du numérateur donc d'un polynôme du second degré (Rappel : il est du signe de a à lextérieur de ses racines s'il en a)
Merci, juste une question, comment justifier que f est définie sur R ?
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 30 Aoû 2013, 22:36
par Frednight » 30 Aoû 2013, 22:36
lorsque tu as une fonction fractionnelle, la seule chose qui pourrait faire qu'elle ne soit pas définissable sur

serait que le dénominateur soit égal à 0. Or celui-ci est strictement positif; la fonction est donc définie pour tout x
-
Toxik
- Membre Naturel
- Messages: 23
- Enregistré le: 30 Aoû 2013, 18:43
-
 par Toxik » 30 Aoû 2013, 22:37
par Toxik » 30 Aoû 2013, 22:37
Frednight a écrit:lorsque tu as une fonction fractionnelle, la seule chose qui pourrait faire qu'elle ne soit pas définissable sur

serait que le dénominateur soit égal à 0. Or celui-ci est strictement positif; la fonction est donc définie pour tout x
Merci beaucoup
-
Toxik
- Membre Naturel
- Messages: 23
- Enregistré le: 30 Aoû 2013, 18:43
-
 par Toxik » 31 Aoû 2013, 00:54
par Toxik » 31 Aoû 2013, 00:54
J'ai encore un petit soucis pour la question 3, j'ai utilisé la formule
(x-a)+f(a))
et je trouve comme équation de la tangente en 2

.
Je trouve que le résultat est bizarre avec la visualisation graphique
Merci

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 31 Aoû 2013, 03:28
par capitaine nuggets » 31 Aoû 2013, 03:28
Salut !
Ouais, t'as dû faire une erreur de calculs.
Tu dois trouver
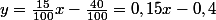
.
Je te laisse refaire correctement tes calculs.
-
Toxik
- Membre Naturel
- Messages: 23
- Enregistré le: 30 Aoû 2013, 18:43
-
 par Toxik » 31 Aoû 2013, 11:06
par Toxik » 31 Aoû 2013, 11:06
capitaine nuggets a écrit:Salut !
Ouais, t'as dû faire une erreur de calculs.
Tu dois trouver
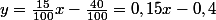
.
Je te laisse refaire correctement tes calculs.
Pourrais tu me mettre tout le calcul car je l'ai recalculé 3 fois et je tombe toujours sur le mauvais résultat
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 31 Aoû 2013, 14:13
par titine » 31 Aoû 2013, 14:13
Je crois que capitaine nuggets a fait une erreur car en effet f'(2) = 0,23 et pas 0,15
-
Toxik
- Membre Naturel
- Messages: 23
- Enregistré le: 30 Aoû 2013, 18:43
-
 par Toxik » 31 Aoû 2013, 14:34
par Toxik » 31 Aoû 2013, 14:34
Avec ma calculatrice, je trouve le même résultat que lui, mais par le calcul c'est totalement différent.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 31 Aoû 2013, 14:45
par Ericovitchi » 31 Aoû 2013, 14:45
c'est simple, f'(2)=0.15 et f(2)=-0.1 donc l'équation de la tangente c'est y=0.15(x-2)-0.1 donc y=0.15x-0.4

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 166 invités

