Démonstration

[tchetchene]

bonjour,
je suis une formation par correspondance,et je n'arrive pas à démontrer une propriété:
a/b=rc[(a²+c²)/(b²+d²)]
qui pourrait m'aider? merci d'avance

[ampholyte]

Bonjour,

Peux-tu mettre la propriété complète ?

Dans quel domaine sont a, b, c, d, r ?

Copie complètement l'énoncé cela sera plus simple.

[tchetchene]

démontrer la propriété si a/b=c/d :

a/b=racine carré de [(a²+c²)/(b²+d²)]

c'est tout ce que j'ai

[ampholyte]

Ha c'est déjà mieux =).

Partons du résultat :



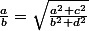
On élève au carré :



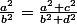
Produit en croix :



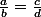
Je te laisse terminer, tu développes et tu pourras factoriser certain terme par a². Tu devrais pouvoir retomber sur en prenant la racine.

[tchetchene]

tout simplement,merci beaucoup

[chan79]

démontrer la propriété si a/b=c/d :

a/b=racine carré de [(a²+c²)/(b²+d²)]

c'est tout ce que j'ai

salut
pose k=a/b=c/d
mais ça marche si tous les nombres sont positifs

avec a=1, b=-1, c=1, d=-1 c'est faux

[Black Jack]

salut
pose k=a/b=c/d
mais ça marche si tous les nombres sont positifs

avec a=1, b=-1, c=1, d=-1 c'est faux

Ou tous négatifs ...
Et aussi à la condition que b et d soient non nuls. :lol3:

:zen:

[chan79]

Ou tous négatifs ...
Et aussi à la condition que b et d soient non nuls. :lol3:

:zen:

oui, on est d'accord