Bonsoir,
Je suis bloqué dans un exercice sur les suites:
F(k)=1/[(k)(k+1)(k+2)]
On me demande de décomposer en éléments simples;
je trouve : F(k)=1/2k -1/(k+1) +1/[2(k+2)]
Ensuite on me demande de calculer Un= somme de 1 à n de F(k) à l'aide de la décomposition précédente.
Et c'est ici que je bloque.
Merci d'avance pour vos réponses!
Exercice suite
8 messages
- Page 1 sur 1
mat5656 a écrit:Bonsoir,
Je suis bloqué dans un exercice sur les suites:
F(k)=1/[(k)(k+1)(k+2)]
On me demande de décomposer en éléments simples;
je trouve : F(k)=1/2k -1/(k+1) +1/[2(k+2)]
Ensuite on me demande de calculer Un= somme de 1 à n de F(k) à l'aide de la décomposition précédente.
Et c'est ici que je bloque.
Merci d'avance pour vos réponses!
Salut
Regarde en suivant des diagonales; ça se simplifie bien ...
Bonjour
On peut écrire=\frac{1}{2k} -\frac{1}{k+1} +\frac{1}{2(k+2)}=[\frac{1}{2k} -\frac{1}{2(k+1)}] +[\frac{1}{2(k+2)}-\frac{1}{2(k+1)}])
En posant=\frac{1}{2k} -\frac{1}{2(k+1)}) et
et =\frac{1}{2(k+2)}-\frac{1}{2(k+1)}) , alors
, alors =G(k)+H(k)) et l'on déduit:
et l'on déduit:
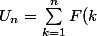=\sum_{k=1}^n(G(k)+H(k))=(\sum_{k=1}^nG(k))+(\sum_{k=1}^nH(k)))
Les deux sommes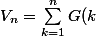) et
et 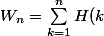) sont simples à calculer.
sont simples à calculer.
Remarques.
J'ai plus ou moins suivi l'indication de jlb, en la détaillant un peu mais peut-être sous une forme.
mat5656 a écrit:Bonsoir,
F(k)=1/[(k)(k+1)(k+2)]
je trouve : F(k)=1/2k -1/(k+1) +1/[2(k+2)]
On peut écrire
En posant
Les deux sommes
Remarques.
J'ai plus ou moins suivi l'indication de jlb, en la détaillant un peu mais peut-être sous une forme.
mat5656 a écrit:Du coup maintenant je trouve:
Somme de 1 à n de F(k)= 1/4 - 1/[(k+1)(k+2)]
Ensuite on me demande la limite en +;)
C'est donc 1/4.
Petite erreur de calcul dans Somme de 1 à n de F(k)= 1/4 - 1/[(k+1)(k+2)],
Somme de 1 à n de F(k)= 1/4 - 1/[2(k+1)(k+2)]
La limite quand n tend vers l'infini reste évidemment la même
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : maths4ever et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
