Incompréhension d'un exemple seconde trigonométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lampetie
- Messages: 3
- Enregistré le: 05 Mai 2013, 19:52
-
 par lampetie » 05 Mai 2013, 19:54
par lampetie » 05 Mai 2013, 19:54
Bonjour,
Je suis en seconde, et je viens solliciter votre aide pour un exemple dans mon livre qui m'échappe. Je viens tout juste de commencer les révisions et j'ai un faible niveau en mathématiques, donc il est possible que la solution soit évidente
Voici un scan de l'énoncé :

Comment font-ils pour passer de cos(pi / 6) à racine3 / 2?
Votre aide me serait très utile, je vous remercie d'avance !
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 05 Mai 2013, 19:57
par XENSECP » 05 Mai 2013, 19:57
lampetie a écrit:
Comment font-ils pour passer de cos(pi / 6) à cos( racine3 / 2)?
} = \frac{\sqrt{3}}{2})
plutôt

Bon c'est une des valeurs classiques à connaître par coeur

-
lampetie
- Messages: 3
- Enregistré le: 05 Mai 2013, 19:52
-
 par lampetie » 05 Mai 2013, 20:04
par lampetie » 05 Mai 2013, 20:04
Je m'excuse pour l'erreur de copie et merci pour ton aide :we:
C'était donc une valeur à connaître ? Dans ce cas, pourquoi précisent-ils que cos(pi/6) = cos de l'angle AOM ? Je n'y comprends rien !
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 05 Mai 2013, 20:16
par XENSECP » 05 Mai 2013, 20:16
Bah c'est la définition de l'angle... Je vois pas où est le problème.
-
lampetie
- Messages: 3
- Enregistré le: 05 Mai 2013, 19:52
-
 par lampetie » 05 Mai 2013, 20:21
par lampetie » 05 Mai 2013, 20:21
C'est le "d'où" d'après qui me laissait penser que la réponse devait venir de l'égalité précédente
Je précise aussi qu'il n'y a nulle part dans le livre de tableau de valeurs à connaitre, et que dans l'exercice suivant, on nous demande de déduire cos de x et sin de x pour des valeurs comme x=3pi/4, ou x=7pi/6
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 05 Mai 2013, 21:43
par Robic » 05 Mai 2013, 21:43
Oui, le "d'où" indique que ça vient du théorème précédent. C'était quoi le théorème précédent ? C'est peut-être le point clé.
-
mathelot
 par mathelot » 06 Mai 2013, 08:40
par mathelot » 06 Mai 2013, 08:40
bonjour,
i) sur le cercle trigonométrique, les longueurs d'arc servent à mesurer les angles au centre
ii) dans l'enroulement trigonométrique, les points du cercle ont une abscisse curviligne (abscisse sur une ligne courbe, d'origine A) et l'on démontre que le point d'abscisse curviligne
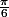
a pour coordonnées cartésiennes
)
dans le repère orthonormé direct de 1er vecteur de base
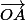
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 06 Mai 2013, 11:35
par Robic » 06 Mai 2013, 11:35
OK, donc effectivement le "d'où" provient de cette propriété. Le raisonnement, c'est :
- On sait (normalement) que le point M associé à l'angle

a pour coordonnées cartésiennes
)
.
- Ici, le point M est associé à l'angle
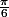
, il a donc pour coordonnées cartésiennes
)
.
- Le théorème précédent indique qu'il a pour coordonnées cartésiennes
)
.
-
D'où :

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités

