Fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 11:12
par F@ntin » 17 Avr 2013, 11:12
mcar0nd a écrit:Attention, il y a deux solutions.
Pour t'en rendre compte regarde, pour la e).
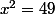
, en passant 49 à gauche, tu as

, là tu reconnais une identité remarquable
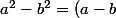(a+b))
donc tu factorise et tu te retrouves avec
(x+7)=0)
, à partir de là, tu trouves facilement les
deux solutions qui sont x=7 ou x=-7.
Fais pareil pour la f maintenant.

Donc tu veux dire que x=7 ou x=-7 c'est ma solution au e.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 17 Avr 2013, 11:12
par mcar0nd » 17 Avr 2013, 11:12
F@ntin a écrit:Donc tu veux dire que x=7 ou x=-7 c'est ma solution au e.
Oui, je veux bien dire ça.
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 11:12
par F@ntin » 17 Avr 2013, 11:12
Ben pour f. c'est x=9 et x=-9 ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 17 Avr 2013, 11:15
par mcar0nd » 17 Avr 2013, 11:15
F@ntin a écrit:Ben pour f. c'est x=9 et x=-9 ?
Oui, c'est bien ça pour la f.
Alors maintenant, pour la première équation, tu trouves quoi?
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 11:31
par F@ntin » 17 Avr 2013, 11:31
mcar0nd a écrit:Oui, c'est bien ça pour la f.
Alors maintenant, pour la première équation, tu trouves quoi?
Ben pour la première équations je sais pas comment vous allez que je fasse ;(
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 17 Avr 2013, 11:35
par mcar0nd » 17 Avr 2013, 11:35
F@ntin a écrit:Ben pour la première équations je sais pas comment vous allez que je fasse ;(
Tu peux me tutoyer.

Donc ton équation, c'est
(7x-1)}{(6x+2)(8x-2)}=0)
et tu sais que
(8x-2)) doit toujours
doit toujours être différent de 0.
Tu dois donc en fait résoudre
(7x-1)=0)
.
Tu comprends l'idée ou pas?
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 11:47
par F@ntin » 17 Avr 2013, 11:47
mcar0nd a écrit:Tu peux me tutoyer.

Donc ton équation, c'est
(7x-1)}{(6x+2)(8x-2)}=0)
et tu sais que
(8x-2)) doit toujours
doit toujours être différent de 0.
Tu dois donc en fait résoudre
(7x-1)=0)
.
Tu comprends l'idée ou pas?
D'accord. Et a la fin sa doit donne S{ } ?
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 11:49
par F@ntin » 17 Avr 2013, 11:49
Mais comment je fais je calcule [(3x+1)=0 ou (7x-1)=0] ou [(3x+1)(7x-1)=0] ?
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 12:13
par F@ntin » 17 Avr 2013, 12:13
Pour g. (x-3)²=25
x=8 et x=-8
?
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 17 Avr 2013, 12:18
par Archibald » 17 Avr 2013, 12:18
F@ntin a écrit:Mais comment je fais je calcule [(3x+1)=0 ou (7x-1)=0] ou [(3x+1)(7x-1)=0] ?
Un produit est nul lorsqu'au moins un de ses termes est nul. Donc tu résous
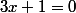
puis
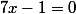
pour avoir ton couple de solution
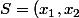)
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 17 Avr 2013, 12:21
par mcar0nd » 17 Avr 2013, 12:21
F@ntin a écrit:Pour g. (x-3)²=25
x=8 et x=-8
?
Non, c'est faux. Il faut que tu factorise le membre de gauche dans l'équation équivalente à le tienne qui est
^2-25=0)
en utilisant une identité remarquable.

-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 17 Avr 2013, 12:25
par Archibald » 17 Avr 2013, 12:25
F@ntin a écrit:Pour g. (x-3)²=25
x=8 et x=-8
?
^2=25 \quad \longleftrightarrow \quad (x-3)^2 ~ = ~ 5^2 \quad \longleftrightarrow \quad x-3 = 5 \quad \longleftrightarrow \quad x=8)
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 12:29
par F@ntin » 17 Avr 2013, 12:29
Archibald a écrit:Un produit est nul lorsqu'au moins un de ses termes est nul. Donc tu résous
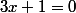
puis
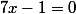
pour avoir ton couple de solution
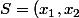)
Donc je trouve x=-1/3 et x=1/7
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 12:30
par F@ntin » 17 Avr 2013, 12:30
Archibald a écrit:^2=25 \quad \longleftrightarrow \quad (x-3)^2 ~ = ~ 5^2 \quad \longleftrightarrow \quad x-3 = 5 \quad \longleftrightarrow \quad x=8)
Merci donc mon résultat et juste 8
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 12:31
par F@ntin » 17 Avr 2013, 12:31
Pouvez-vous m'aider pour les deux autres. C'est les plus complexe pour moi..
-
arutha67
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Avr 2013, 14:42
-
 par arutha67 » 17 Avr 2013, 12:33
par arutha67 » 17 Avr 2013, 12:33
Ce n'est pas nécessairement faux !!
Pas besoin d'identité remarquable !!
(x-3)²>0 on peut donc composer par la fonction racine en n'oubliant pas que racine(x²)= x ou -x
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 12:33
par F@ntin » 17 Avr 2013, 12:33
arutha67 a écrit:Ce n'est pas nécessairement faux !!
Pas besoin d'identité remarquable !!
(x-3)²>0 on peut donc composer par la fonction racine en n'oubliant pas que racine(x²)= x ou -x
D'accord. Merci

-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 17 Avr 2013, 12:36
par mcar0nd » 17 Avr 2013, 12:36
Archibald a écrit:^2=25 \quad \longleftrightarrow \quad (x-3)^2 ~ = ~ 5^2 \quad \longleftrightarrow \quad x-3 = 5 \quad \longleftrightarrow \quad x=8)
Je suis pas vraiment d'accord avec ça.
^2=25 \Longleftrightarrow (x-3)^2-25=0 \Longleftrightarrow [(x-3)-5][(x-3)+5]=0 \Longleftrightarrow (x-8)(x+2)=0)
, les deux solutions sont donc
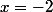
ou
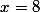
.
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 17 Avr 2013, 12:43
par Archibald » 17 Avr 2013, 12:43
Oui, vous avez totalement raison. je suis allé un peu vite en besogne, résultat : une solution évidente omise.
F@ntin a écrit:Donc je trouve x=-1/3 et x=1/7
C'est exact.
-
F@ntin
- Membre Naturel
- Messages: 51
- Enregistré le: 09 Sep 2012, 09:33
-
 par F@ntin » 17 Avr 2013, 12:47
par F@ntin » 17 Avr 2013, 12:47
Donc je marque S{-1/3;1/7}
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
, en passant 49 à gauche, tu as
, là tu reconnais une identité remarquable
donc tu factorise et tu te retrouves avec
, à partir de là, tu trouves facilement les deux solutions qui sont x=7 ou x=-7.
