Dérivée/primitive simple

[Dante0]

Bonjour,

Je dois dériver

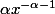
A première vue je dirais mais c'est pourquoi ?

Merci !

[annick]

Bonjour,
s'il n'y a pas d'erreur dans ton énoncé et que l'on parle bien de dérivée, je dirais que ton expression est juste et le résultat que l'on te donne faux.
Mais es-tu bien sûr des énoncés ?

[homeya]

Bonjour,

Pour moi, c'est .

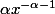
Cordialement.

[homeya]

Oops ... nos réponses se sont croisées !

[Dante0]

Oui sur !

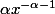
Comment trouver la primitive de je veux faire le chemin inverse, histoire de ne pas confondre les formules de dérivées et celles de primitives.

[annick]

Une primitive de x^m est (x^(m+1))/(m+1)

Ici, primitive de -ax^(-a-1)=-ax^(-a-1+1)/(-a-1+1)+k=-ax^(-a)/-a=x^(-a)+k (dans ton cas, k=1)

[annick]

Une primitive de x^m est (x^(m+1))/(m+1)

Ici, primitive de ax^(-a-1)=ax^(-a-1+1)/(-a-1+1)+k=ax^(-a)/-a=-x^(-a)+k (dans ton cas, k=1)