Trinôme du second degré

[Mr.Joker]

Bonsoir,

J'ai passé beaucoup de temps sur une question de mon DM mais, je ne comprend toujours pas comment la résoudre. J'aurais bien besoin de votre aide s'il vous plait.

Soit le trinôme (polynôme de degré 2) .
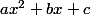
Montrer que est racine de si, et seulement si, se factorise par .

Merci beaucoup.

[Vahinerii]

La racine de P de degré 2 est x1 telle que P(x1)=0 ce qui fait que P(x)= a(x-x1)Q(x) où Q a le degré 1...

[Black Jack]

Si x1 est racine de T(x) = ax²+bx+c, alors : a.x1²+b.x1+c = 0

T(x) - 0 = ax²+bx+c - (a.x1²+b.x1+c)

T(x) = a(x²-x1²) + b(x-x1)

T(x) = a(x-x1)(x+x1) + b(x-x1)

T(x) = (x-x1).(a(x+x1)-b)

Et donc : x1 est racine de T(x) = ax²+bx+c ==> T(x) se factorise par (x-x1) (1)
***
Si T(x) se factorise par (x-x1), alors ...

Il faut poursuivre et arriver à montrer que : T(x) se factorise par (x-x1) ==> x1 est racine de T(x) (2)
***

Et (1) et (2) --->

x1 est racine de T(x) = ax²+bx+c <==> T(x) se factorise par (x-x1)

:zen: