Bonsoir, j'ai un dm de spé maths, j'ai pas encore tout fait, mais la réponse à la première question me parais si simple que j'en doute. Dites-moi svp ce que vous en penser.
Il s'agit de résoudre dans Z le sustème (S):{n congru à 13 mod(19)
{n congru à 6 mod(12)
1/ Démontrer qu'il existe un couple (u, v) d'entiers relatifs tels 19u+12v=1
( on ne demande pas de donner un exemple d'un tel couple)
Ma réponse est: PGCD(19,12)=1, d'après l'identité de Bezout, il existe un couple (u,v) d'entiers relatifs/ 19u+12u=1
Est-ce suffisant à votre avis?
2/ vérifier que pour un tel couple de nombre, le nombre N=13*12v+6*19u est une solution de (S)
je pense déterminer u et v puis remplacer dans N pour vérifier. Est-ce cela?
Merci de m'éclairer svp
Spé maths
4 messages
- Page 1 sur 1
Salut !
1) oui, ca suffit.
2) (u,v) vérifie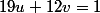 donc
donc 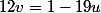 . Montralors que
. Montralors que 
jeaden a écrit:Bonsoir, j'ai un dm de spé maths, j'ai pas encore tout fait, mais la réponse à la première question me parais si simple que j'en doute. Dites-moi svp ce que vous en penser.
Il s'agit de résoudre dans Z le sustème (S):{n congru à 13 mod(19)
{n congru à 6 mod(12)
1/ Démontrer qu'il existe un couple (u, v) d'entiers relatifs tels 19u+12v=1
( on ne demande pas de donner un exemple d'un tel couple)
Ma réponse est: PGCD(19,12)=1, d'après l'identité de Bezout, il existe un couple (u,v) d'entiers relatifs/ 19u+12u=1
Est-ce suffisant à votre avis?
2/ vérifier que pour un tel couple de nombre, le nombre N=13*12v+6*19u est une solution de (S)
je pense déterminer u et v puis remplacer dans N pour vérifier. Est-ce cela?
Merci de m'éclairer svp
1) oui, ca suffit.
2) (u,v) vérifie
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
jeaden a écrit:Merci capitaine nuggets
De rien :we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
