Problème de topologie

[prepsain]

Bonsoir,

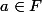
Il y'a quelque chose que je n'arrive pas à comprendre dans un exercice: est un evn, et et un compact, on veut montrer qu'il existe un tel que

Évidement, j'ai le corrigé sous les yeux mais je ne comprends pas: il considère qu'il existe une suite telle que

Je ne sais pas ce qui justifie l’existence de telle qu'il la définit!

Si vous pouvez m'éclairer ce serait super!

Merci

[girdav]

Utilise la définition de l'infimum.

[bentaarito]

Bonsoir,

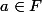
Il y'a quelque chose que je n'arrive pas à comprendre dans un exercice: est un evn, et et un compact, on veut montrer qu'il existe un tel que

Évidement, j'ai le corrigé sous les yeux mais je ne comprends pas: il considère qu'il existe une suite telle que

Je ne sais pas ce qui justifie l’existence de telle qu'il la définit!

Si vous pouvez m'éclairer ce serait super!

Merci

Tu veux montrer qu'il existe y;)F tel que d(x,F)=;) y;)x
Or par définition

Donc pour tout n;)N, il existe y_n;)F tel que
d(x,F););) y_n;)x <d(x,F)+1/(n+1)

En faisant varier n, cela définit une suite (y_n);) telle que y_n;)x ;)d(x,F).
Puisque y_n ;);) x +;) y_n;)x , la suite (y_n) est bornée. Il existe donc une suite extraite (y;)(n)) convergente de limite y.
Puisque (y_;)(n)) est une suite d'éléments du fermé F, on a y;)F.
Puisque y_;)(n);)y et y_;)(n);)x ;)d(x,F) on a aussi y;)x =d(x,F) ( car une norme est continue)

[prepsain]

Tu veux montrer qu'il existe y;)F tel que d(x,F)=;) y;)x
Or par définition

Donc pour tout n;)N, il existe y_n;)F tel que
d(x,F););) y_n;)x <d(x,F)+1/(n+1)

En faisant varier n, cela définit une suite (y_n);) telle que y_n;)x ;)d(x,F).
Puisque y_n ;);) x +;) y_n;)x , la suite (y_n) est bornée. Il existe donc une suite extraite (y;)(n)) convergente de limite y.
Puisque (y_;)(n)) est une suite d'éléments du fermé F, on a y;)F.
Puisque y_;)(n);)y et y_;)(n);)x ;)d(x,F) on a aussi y;)x =d(x,F) ( car une norme est continue)

Merci pour ta réponse, pour la définition je suis d'accord (heureusement pour moi ), apres pourquoi dis-tu que
d(x,F););) y_n;)x <d(x,F)+1/(n+1) ? Pour moi ce n'est pas clair.

Pour la continuité de la norme, je trouve aussi ça dans mon cours mais sans démonstration.....

Ce que je comprends assez bien est que le fameux a est la valeur d'adhérence d'une suite mais la construction reste floue pour moi :mur:

[bentaarito]

d(x,F););) y_n;)x <d(x,F)+1/(n+1)

Comment écris-tu la caractérisation de la borne inf?

Pour la continuité de la norme

Il suffit d'appliquer l'inégalité triangulaire renversée

[prepsain]

Comment écris-tu la caractérisation de la borne inf?



Il suffit d'appliquer l'inégalité triangulaire renversée

Merci bentaarito, tu commences à me rendre le sourire pour l'inégalité triangulaire renversée, je ne vois pas

[bentaarito]

en utilisant le fait que: |;)x;)- ;)y;)| <= ;) x-y ;), tu vois qu'une norme est bien continue :lol3:

[prepsain]

en utilisant le fait que: |;)x;)- y;)| <= x-y , tu vois qu'une norme est bien continue :lol3:

Thanks thanks thansk