Bonsoir,
j'ai un problème avec un exo je ne suis pas sur de ma rédaction et j'aimerais avoir votre avis
Soit f :

\{(0, 0)}

lapplication définie par
 =\frac{x+y}{\sqrt{x^2+y^2})
1. Montrer que f est continue sur

\ {(0, 0)}.
2. Montrer que f nest pas prolongeable par continuité en (0, 0).
1.(x,y)->x+y est continue sur

et donc sur

\ {(0, 0)}.(x,y)->
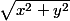
est continue sur

et s'annule en (0,0) , par passage à l'inverse

est continue sur

\ {(0, 0)}.par produit, f est continue sur

\ {(0, 0)}.
2.
=\frac{x}{|x|})
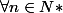
-
=1)
-
=-1)
les suites
}n)
et
}n)
tendent toutes les deux vers (0,0) mais le long de ses suites admettent deux limites différentes donc f nest pas prolongeable par continuité en (0, 0).
je voudrais savoir si c'est tjr correct de procéder de la manière suivante:
=\frac{x}{|x|})
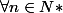
-
=1)
=\frac{2x}{|x|\sqrt{2}}=\frac{sqrt{2}*x}{|x|})
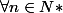
-
=\sqrt{2})
les suites
}n)
et
}n)
tendent toutes les deux vers (0,0) mais le long de ses suites admettent deux limites différentes donc f nest pas prolongeable par continuité en (0, 0).
