Révisions d'intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 03 Déc 2012, 13:40
par Xeno01 » 03 Déc 2012, 13:40
Bonjour tout le monde !
Voila, je passe un examen dans quatre jours, et je n'ai pas compris certaines choses, pourriez vous m'eclairer ?
Intégration par partie :

J'applique la formule, mais y'a mystére, ca bloque ..
Montrez qu'il existe a,b,c tels que pour tout

{2;3}, on a :
^2(x-3)} = \frac {a} {(x-2)^2} + \frac {b} {x-2} + \frac {c} {x-3})
Ici, j'ai essayé de developper, mais je tombe sur une expression horrible impossible a simplifier ( en tout cas j'ai pas reussi ^^ )
Vous pouvez m'aider ? Merci pour votre coopération

-
Anonyme
 par Anonyme » 03 Déc 2012, 13:44
par Anonyme » 03 Déc 2012, 13:44
@Xeno01
Pour calculer

il faut faire
2 Intégrations par parties
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 03 Déc 2012, 13:48
par Xeno01 » 03 Déc 2012, 13:48
Pas bête du tout, je m'y mets de suite :D
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 03 Déc 2012, 14:13
par Xeno01 » 03 Déc 2012, 14:13
est ce que
dx = \bigint_{0}^{1} xdx)
x
dx)
?
Et donc [1/2 x²]x

?
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 03 Déc 2012, 14:24
par Mathusalem » 03 Déc 2012, 14:24
Xeno01 a écrit:est ce que
dx = \bigint_{0}^{1} xdx)
x
dx)
?
Et donc [1/2 x²]x

?
Est-ce que
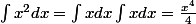
ou plutôt
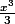
?
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 03 Déc 2012, 14:54
par Xeno01 » 03 Déc 2012, 14:54
Je pense que ca ferait (x^4)/4, non ?
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 03 Déc 2012, 15:16
par Mathusalem » 03 Déc 2012, 15:16
Donne moi la dérivée de x^3/3. Ensuite, donne moi une primitive de x^2.
Puis, donne moi la dérivée de x^4/4. Tu devrais voir qu'il y a un problème.
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 03 Déc 2012, 15:30
par Xeno01 » 03 Déc 2012, 15:30
Primitive de x^2 = 1/3x^3
Dérivée x^3/3 =x²
Dérivée x^4/4 = x^3
Je deviens fou .. Je suis censé voir qu'il faut encore faire une inté. par partie c'est ca ? Et que multiplier simplement deux intégrales n'est pas possible?
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 03 Déc 2012, 15:46
par Xeno01 » 03 Déc 2012, 15:46
Je crois avoir trouvé mais je suis sur de rien x)

=

-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 03 Déc 2012, 16:16
par Mathusalem » 03 Déc 2012, 16:16
Oui.. en particulier tu vois que

Or, si tu sépares

. Tu n'as donc pas le droit de séparer. Et ton résultat est faux.
Comment t'y prends-tu ? Est-ce que tu réussis à trouver déjà une primitive de la fonction ? C'est-à-dire une expression qui lorsqu'elle est dérivée te donne
)
?
Si tu n'y arrives pas tu peux faire l'intégration par partie. Dans ce cas, explique comment tu la fais.
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 03 Déc 2012, 17:04
par Xeno01 » 03 Déc 2012, 17:04
Merde x)
Et bien j'ai fait l'intégration par partie de x² et celle de
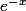
..
Ce qui me donne :
([x.e^-^1] - \bigint_{0}^{1} x.x(-e^-^x))
Je suis bien parti ? Si non, tu pourrais me corriger explicitement, que j'avance dans mes révisions ?
Merci !
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 03 Déc 2012, 17:45
par Mathusalem » 03 Déc 2012, 17:45
Xeno01 a écrit:Merde x)
Et bien j'ai fait l'intégration par partie de x² et celle de
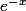
..
Ce qui me donne :
([x.e^-^1] - \bigint_{0}^{1} x.x(-e^-^x))
Je suis bien parti ? Si non, tu pourrais me corriger explicitement, que j'avance dans mes révisions ?
Merci !
Une intégration par partie se fait ainsi :
Tu prends un produit de fonctions u(x)v(x).
Tu sais que
v(x)]' = u'(x)v(x) + u(x)v'(x))
Donc,
v(x)dx = \left[u(x)v(x)\right]_a^b - \int \limits_{a}^b u(x)v'(x)dx)
Donc l'idée c'est de changer ton intégrale en un truc plus facile par cette formule, qui s'appelle l'intégration par partie.
Ici, tu choisis v(x) = x^2, u'(x) = e^{-x}, donc v'(x) = 2x et u(x) = -e^{-x}. Donc en remettant dans la formule d'IPP, on a

Tu sais facilement évaluer le terme entre crochets. Donc tu réduis ton intégrale de x^2e{-x} à 2xe^{-x}. Tu peux denouveau appeler 2x = v(x) et u'(x) = e^{-x} et tu recommences. Est-ce que tu y arrives ?
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 04 Déc 2012, 11:49
par Xeno01 » 04 Déc 2012, 11:49
J'ai trouvé :

Je t'en prie, dis moi que c'est bon x)
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 04 Déc 2012, 18:01
par Mathusalem » 04 Déc 2012, 18:01
Mets-ici le calcul que tu fais
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 04 Déc 2012, 20:20
par Xeno01 » 04 Déc 2012, 20:20
] - \bigint -2x.e^-^x)
(1ere inté. par partie )
=>
] - [[2x.(-e^-^x)] - \bigint 2e^-^x ])
(2e inté par partie)
=>
] - [[2x.(-e^-^x)] - 2[-e^-^x])
Bon et puis la je calcule F(1) et F(0) pour chaque facteurs
Mistake ?
-
Xeno01
- Membre Naturel
- Messages: 50
- Enregistré le: 15 Avr 2010, 14:02
-
 par Xeno01 » 06 Déc 2012, 12:09
par Xeno01 » 06 Déc 2012, 12:09
SVP, mon controle est demain, up ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
