Problème compréhension formule
24 messages
- Page 1 sur 2 - 1, 2
problème compréhension formule
Bonjour à tous !
je suis une élève de Terminale, j'ai entamé un chapitre sur les fonctions exponentielles et mon professeur a fait une parenthèse pour nous donner une formule de dérivation nouvelle qui pourrait nous aider, il s'agit de celle ci :
[f(ax+b)]' = a*f'(ax+b)
j'ai du mal à comprendre quelle est la différence entre [f(ax+b)]' et f'(ax+b)
quelqu'un pourrait-il m'expliquer s'il vous plait ?
Merci d'avance,
olapehtna
je suis une élève de Terminale, j'ai entamé un chapitre sur les fonctions exponentielles et mon professeur a fait une parenthèse pour nous donner une formule de dérivation nouvelle qui pourrait nous aider, il s'agit de celle ci :
[f(ax+b)]' = a*f'(ax+b)
j'ai du mal à comprendre quelle est la différence entre [f(ax+b)]' et f'(ax+b)
quelqu'un pourrait-il m'expliquer s'il vous plait ?
Merci d'avance,
olapehtna
Bonjour
En fait il n'y a pas de différence. J'utilise aussi parfois cette façon de noter la dérivée simplement pour mettre en évidence la prime.
En effet, la prime est toute petite et on pourrait ne pas la voir entre le f et la parenthèse.
En plus, c'est important de bien comprendre que f'(a.x+b) et la dérivée de toute l'expression, c'est à dire de la fonction f(ax+b).
En notant\right]^') , cela permet d'appuyer sur le fait que l'on cherche à exprimer la dérivée d'une expression du type fonction d'un polynôme en x.
, cela permet d'appuyer sur le fait que l'on cherche à exprimer la dérivée d'une expression du type fonction d'un polynôme en x.
On souligne ainsi le fait que l'expression de la dérivée de la même fonction f pour un autre type d'image pourrait être différente.
C'est bien le cas, l'expression indiquée n'est pas valable pour par exemple dériver)) !
!
En fait il n'y a pas de différence. J'utilise aussi parfois cette façon de noter la dérivée simplement pour mettre en évidence la prime.
En effet, la prime est toute petite et on pourrait ne pas la voir entre le f et la parenthèse.
En plus, c'est important de bien comprendre que f'(a.x+b) et la dérivée de toute l'expression, c'est à dire de la fonction f(ax+b).
En notant
On souligne ainsi le fait que l'expression de la dérivée de la même fonction f pour un autre type d'image pourrait être différente.
C'est bien le cas, l'expression indiquée n'est pas valable pour par exemple dériver
Très bonne question.
Je crois surtout que c'est moi qui est mal compris la question et qui est donc mal formulée ma première réponse.
Je reprend donc.
A toute fonction f continue, il existe une et une seule fonction f' dérivée. Pour chaque point du domaine de définition et sous réserve de continuïté, cette fonction dérivée donne le sens et le taux de variation de la fonction f.
Il est possible de donner pour tout point de valeur x du domaine de définition la valeur y image de x par la fonction f que l'on note y=f(x).
De la même manière, à tout point z du même domaine de définition, il est possible de donner la valeur de la dérivée t=f'(z).
Cela est vai aussi au point x, on peut donc donner la valeur de la dérivée au point z=x en calculant la valeur t=f'(x).
Si maintenant , au lieu de considèrer le point x, on considère le point a.x+b où a et b sont deux paramètres. On a alors t=f'(a.x+b) la valeur de la dérivée de la fonction f au point a.x+b
C'est donc se que rprésente) , c'est la valeur de la dérivée au point
, c'est la valeur de la dérivée au point 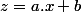
Et c'est là que j'ai mal répondu dans mon premier post.
Il y a bien une diffèrence entre [f(a.x+b)]' et f'(a.x+b) car, en fait si f'(a.x+b) n'est que la valeur de la dérivée au point a.x+b, à l'inverse, la notation [f(a.x)+b]' veut désigner l'expression (ou la formule) de la fonction f dérivée en tous points de la forme a.x+b
En effet, il faut faire la diffèrence entre la valeur en un point donné et l'expression générale qui va permettre d'exprimer la formule de la fonction dérivée.
En effet, jusqu'ici, je n'ai pas mentionné ou indiqué d'expression ou donné la formule qui définie f. Donc f' désine la dérivée de f sans pour autant en donner une expression ou une formule.
Par contre, [f(a.x+b)]' désigne l'expression ou la formule de la dérivée. Il s'avère de plus que cette expression, dans le cas d'un polynôme a.x+b, s'exprime en fonction d'une valeur de la dérivée f'.
Je suis désolé d'avoir répondu maladroitement la première fois. :triste:
Il y a bien donc une différence.
Mais il ne faut pas voir le signe égal exactement comme celui d'une égalité, c'est plus le symbole d'une définition ou d'une équivalence :
« L'expression de la dérivée de la fonction f en tous points donnés par le polynôme a.x+b est de la forme a.f'(a.x+b) » qui s'écrit «]'=a.f'(a.x+b)) »
»
On remarquera que cette formule est cohérente :
]' = [f(1.x+0)]' = 1.f'(1.x+0) = f'(x)) on a bien
on a bien ]'=f'(x))
Je crois surtout que c'est moi qui est mal compris la question et qui est donc mal formulée ma première réponse.
Je reprend donc.
A toute fonction f continue, il existe une et une seule fonction f' dérivée. Pour chaque point du domaine de définition et sous réserve de continuïté, cette fonction dérivée donne le sens et le taux de variation de la fonction f.
Il est possible de donner pour tout point de valeur x du domaine de définition la valeur y image de x par la fonction f que l'on note y=f(x).
De la même manière, à tout point z du même domaine de définition, il est possible de donner la valeur de la dérivée t=f'(z).
Cela est vai aussi au point x, on peut donc donner la valeur de la dérivée au point z=x en calculant la valeur t=f'(x).
Si maintenant , au lieu de considèrer le point x, on considère le point a.x+b où a et b sont deux paramètres. On a alors t=f'(a.x+b) la valeur de la dérivée de la fonction f au point a.x+b
C'est donc se que rprésente
Et c'est là que j'ai mal répondu dans mon premier post.
Il y a bien une diffèrence entre [f(a.x+b)]' et f'(a.x+b) car, en fait si f'(a.x+b) n'est que la valeur de la dérivée au point a.x+b, à l'inverse, la notation [f(a.x)+b]' veut désigner l'expression (ou la formule) de la fonction f dérivée en tous points de la forme a.x+b
En effet, il faut faire la diffèrence entre la valeur en un point donné et l'expression générale qui va permettre d'exprimer la formule de la fonction dérivée.
En effet, jusqu'ici, je n'ai pas mentionné ou indiqué d'expression ou donné la formule qui définie f. Donc f' désine la dérivée de f sans pour autant en donner une expression ou une formule.
Par contre, [f(a.x+b)]' désigne l'expression ou la formule de la dérivée. Il s'avère de plus que cette expression, dans le cas d'un polynôme a.x+b, s'exprime en fonction d'une valeur de la dérivée f'.
Je suis désolé d'avoir répondu maladroitement la première fois. :triste:
Il y a bien donc une différence.
Mais il ne faut pas voir le signe égal exactement comme celui d'une égalité, c'est plus le symbole d'une définition ou d'une équivalence :
« L'expression de la dérivée de la fonction f en tous points donnés par le polynôme a.x+b est de la forme a.f'(a.x+b) » qui s'écrit «
On remarquera que cette formule est cohérente :
Bonjour,
) est l'image de
est l'image de 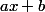 par
par  .
.
Le soucis doit venir ensuite de la compréhension de la notation,) est l'image de
est l'image de 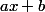 par
par  alors qu'en écrivant
alors qu'en écrivant ]) on sous entend que l'on travaille sur une fonction qui est la composé de
on sous entend que l'on travaille sur une fonction qui est la composé de  avec la fonction qui a
avec la fonction qui a  associe
associe 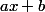 que l'on peut appeler
que l'on peut appeler  . Et c'est cette fonction composée
. Et c'est cette fonction composée 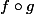 que l'on dérive. Pour rapidement expliquer, si
que l'on dérive. Pour rapidement expliquer, si  est la fonction
est la fonction  alors
alors 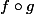 est
est  , si
, si  est la fonction
est la fonction  alors
alors 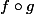 est
est ^3 + 3) etc ...
etc ...
De mon point de vue, écrire]') =
= ) n'est pas correct, en effet
n'est pas correct, en effet ]') est une fonction : la fonction dérivée de
est une fonction : la fonction dérivée de 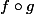 alors que
alors que ) est un nombre : l'image de
est un nombre : l'image de 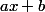 par
par 
il aurait fallu écrire]'(x)) =
= ) c'est à dire en français :
c'est à dire en français :
L'image de par la dérivée de
par la dérivée de 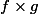 est égale à
est égale à  l'image de
l'image de 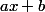 par la dérivée de f.
par la dérivée de f.
Un exemple concret :
Prenons donc
donc 
On cherche]'(x)) c'est à dire
c'est à dire^2]'(x)) soit
soit ) et en dérivant on a
et en dérivant on a 
La formule nous dit que c'est égal à) c'est à dire
c'est à dire ) soit
soit ) et on retombe bien sur le même résultat.
et on retombe bien sur le même résultat.
Le soucis doit venir ensuite de la compréhension de la notation,
De mon point de vue, écrire
il aurait fallu écrire
L'image de
Un exemple concret :
Prenons
On cherche
La formule nous dit que c'est égal à
tout d'abord, merci pour vos réponses très développées, c'est vraiment appréciable ! :++:
je vais essayer de développer une fonction pour vérifier si j'ai bien compris :
prenons par exemple (7x-4)²
g(x) = (7x-4)²
or f(x) = g(x)
donc f(x) = (7x-4)² => f(ax+b) = x²
et g'(x) = a*f'(ax+b) => g'(x) = 7 * (2*(7x+4)) = 7*(14x+8) = 98x+56
ai-je bien compris ? :we:
je vais essayer de développer une fonction pour vérifier si j'ai bien compris :
prenons par exemple (7x-4)²
g(x) = (7x-4)²
or f(x) = g(x)
donc f(x) = (7x-4)² => f(ax+b) = x²
et g'(x) = a*f'(ax+b) => g'(x) = 7 * (2*(7x+4)) = 7*(14x+8) = 98x+56
ai-je bien compris ? :we:
edit : j'ai fais une petite erreur de signe : j'ai écris +4 au lieu de -4 ce qui modifie le signe de 56, mais outre cette erreur dinattention je pense avoir compris.
est ce que vous pensez que j'ai le bon raisonnement ? et manque t il ou y a t il quelque chose de dispensable dans mon calcul ?
merci
est ce que vous pensez que j'ai le bon raisonnement ? et manque t il ou y a t il quelque chose de dispensable dans mon calcul ?
merci
Tu dérives bien la fonction dans ta dernière mais il y a un soucis dans les premières choses que tu écris. En effet, f est différente de g et la fonction que l'on cherche à dérivé est ni l'une ni l'autre mais la composée des deux.
On veut dériver^2)
C'est la fonction composée]) avec
avec  . On peut aussi écrire cette fonction
. On peut aussi écrire cette fonction 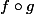 avec
avec  .
.
Donc la dérivée vaut = 7 \times [2x](7x-4) = 7 \times 2.(7x-4))
On veut dériver
C'est la fonction composée
Donc la dérivée vaut
Oui, c'est presque juste, sauf que c'est un peu embrouillé car il y a confusion entre les fonction f et g. Et aussi un erreur de signe (mais ça c'est pas grave aujourd'hui)
En fait, c'est simple, il n'y a pas à faire de mélange entre les f et les g.
Si l'on considère la fonction = (7x-4)^2) définie pour tout réel x.
définie pour tout réel x.
On veut calculer la dérivée) :
:
= [(7x-4)^2]') (*)
(*)
Si l'on fait directement, on trouve :
= [(7x-4)^2]'=2(7x-4)(7x-4)'=2(7x-4)(7x)'=2(7x-4)7x'=2(7x-4)7=14.(7x-4))
Mais, on peux aussi utiliser l'astuce indiquée par le prof :
Pour cela nous posons=x^2) pour tout réel x.
pour tout réel x.
Nous savons calculer la dérivée de cette fonction,=2.x) pour tout réel x.
pour tout réel x.
On se rend compte que
= [f(7x-4)]')
Et donc
= [f(7x-4)]' = 7.f'(7x-4) = 7.(2.(7x-4)) = 14.(7x-4))
Nous obtenons bien évidemment le même résultat. :lol3:
Mais alors, pourquoi avoir utiliser cette seconde méthode ??
Ben, l'idée est que cela rend bien service avec certaines fonctions.
Par exemple, une exponentielle.
(*) Voilà pourquoi j'ai affirmé précèdemment qu'il n'y avait pas de diffèrence :hum:
En fait, c'est simple, il n'y a pas à faire de mélange entre les f et les g.
Si l'on considère la fonction
On veut calculer la dérivée
Si l'on fait directement, on trouve :
Mais, on peux aussi utiliser l'astuce indiquée par le prof :
Pour cela nous posons
Nous savons calculer la dérivée de cette fonction,
On se rend compte que
Et donc
Nous obtenons bien évidemment le même résultat. :lol3:
Mais alors, pourquoi avoir utiliser cette seconde méthode ??
Ben, l'idée est que cela rend bien service avec certaines fonctions.
Par exemple, une exponentielle.
(*) Voilà pourquoi j'ai affirmé précèdemment qu'il n'y avait pas de diffèrence :hum:
Tu peux donner un nom à ta fonction (f, g, h etc.) et travailler avec f', g' et h'.
Autrement, lors de ta rédaction, il te suffit de citer les formules de dérivation et de les appliquer directement.
Exemple de rédaction :
:happy3:
Autrement, lors de ta rédaction, il te suffit de citer les formules de dérivation et de les appliquer directement.
Exemple de rédaction :
Question : Soit f(x)=(2x+1)², calculer f'(x)
Réponse : On utilise la propriété : Pour toute fonction dérivable u,.
Ici, on prend. Alors
si bien que
, c'est à dire
:happy3:
Nightmare a écrit:Tu peux donner un nom à ta fonction (f, g, h etc.) et travailler avec f', g' et h'.
Autrement, lors de ta rédaction, il te suffit de citer les formules de dérivation et de les appliquer directement.
Exemple de rédaction :
:happy3:
(ceci étant dis je ne vois pas où est ce que cette formule est utilisée dans la démonstration)
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
