Problème méthode de décomposition
16 messages
- Page 1 sur 1
problème méthode de décomposition
Bonjour,
L'exercice demandé est de démontrer que :
2/(pq) = 1 / (p ((p+q) / 2)) + 1 / (q ((p+q) / 2))
La correction proposée est :
1 / (p ((p+q) / 2)) + 1 / (q ((p+q) / 2)) = (q + p) / (p x q x ((p+q) / 2)) = 2/(pq)
Je suis perdu, je ne comprends pas pourquoi
1 / (p ((p+q) / 2)) + 1 / (q ((p+q) / 2)) = (q + p) / (p x q x ((p+q) / 2)) = 2/(pq)
Pourriez-vous m'éclairer s'il vous plaît ?
Merci d'avance.
Prune 18.
PS : désolé pour le format des écritures fractionnaires mais je ne sais pas comment les poser.
J'espère que c'est plus clair avec les parenthèses.
L'exercice demandé est de démontrer que :
2/(pq) = 1 / (p ((p+q) / 2)) + 1 / (q ((p+q) / 2))
La correction proposée est :
1 / (p ((p+q) / 2)) + 1 / (q ((p+q) / 2)) = (q + p) / (p x q x ((p+q) / 2)) = 2/(pq)
Je suis perdu, je ne comprends pas pourquoi
1 / (p ((p+q) / 2)) + 1 / (q ((p+q) / 2)) = (q + p) / (p x q x ((p+q) / 2)) = 2/(pq)
Pourriez-vous m'éclairer s'il vous plaît ?
Merci d'avance.
Prune 18.
PS : désolé pour le format des écritures fractionnaires mais je ne sais pas comment les poser.
J'espère que c'est plus clair avec les parenthèses.
C'est vrai, de plus je crois que la question d'après n'est pas évidente (montrer que  s'écrit comme somme de deux fractions égyptiennes différentes). Pour info, c'est de la mémoire récente, je faisais travailler un ami sur ce sujet il y a une dizaine de jours :we:
s'écrit comme somme de deux fractions égyptiennes différentes). Pour info, c'est de la mémoire récente, je faisais travailler un ami sur ce sujet il y a une dizaine de jours :we:
prune18 a écrit:Quelles mémoires!En fait comme je passe le concours fin septembre, je fais des sujets d'annales mais les corrections sont parfois trop rapides!
Luc a écrit:C'est vrai, de plus je crois que la question d'après n'est pas évidente (montrer ques'écrit comme somme de deux fractions égyptiennes différentes). Pour info, c'est de la mémoire récente, je faisais travailler un ami sur ce sujet il y a une dizaine de jours :we:
Tout s'explique! J'avoue avoir abandonner les questions suivantes... :s Les sujets sont tout de même très inégalitaires d'un groupement à l'autre!
Luc a écrit:Arg, c'est dommage d'abandonner, à mon avis tu en tireras plus de profit si tu en fais moins, mais en entier (le forum est là pour t'aider dans ce cas là). As-tu une idée pour les décompositions de?
Luc
Je prends en note ton conseil
Je sais bien que le forum est là pour m'aider mais ce sujet est vraiment long, je n'ai pas envie d'abuser du forum :hum:
Sans grande conviction je dirais comme
1 / (1 x ((1+15)/2) + 1 / (15 x ((1+15)/2) ?
Oui, c'est exact! Et que valent respectivement les fractions 1 / (1 x ((1+15)/2) et 1 / (15 x ((1+15)/2)? (il suffit de les écrire sous les formes 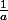 )
)
D'autre part, l'énoncé dit qu'il y a deux décompositions différentes possibles. Tu en as trouvé une. Comment pourrais-tu trouver la deuxième?
Luc
D'autre part, l'énoncé dit qu'il y a deux décompositions différentes possibles. Tu en as trouvé une. Comment pourrais-tu trouver la deuxième?
Luc
prune18 a écrit:
Sans grande conviction je dirais commealors
=
et après je remplace alors p et q :
1 / (1 x ((1+15)/2) + 1 / (15 x ((1+15)/2) ?
Luc a écrit:Oui, c'est exact! Et que valent respectivement les fractions 1 / (1 x ((1+15)/2) et 1 / (15 x ((1+15)/2)? (il suffit de les écrire sous les formes)
D'autre part, l'énoncé dit qu'il y a deux décompositions différentes possibles. Tu en as trouvé une. Comment pourrais-tu trouver la deuxième?
Luc
Je développe donc :
Pour la deuxième solution peut-être serait-il possible de chercher des multiples de 15, comme par exemple 3 et 5 ainsi p=3 et q=5 ?
PS : merci pour vos réponses et vos questions qui me motive à regarder ce problème de plus près et chercher des solutions
prune18 a écrit:Je développe donc :+
+
+
C'est tout bon!
prune18 a écrit:Pour la deuxième solution peut-être serait-il possible de chercher des multiples de 15, comme par exemple 3 et 5 ainsi p=3 et q=5 ?
C'est ça, tu es sur la bonne voie. Il ne reste plus qu'à l'écrire, ça donne quelles fractions? :we:
prune18 a écrit:PS : merci pour vos réponses et vos questions qui me motive à regarder ce problème de plus près et chercher des solutions
Tant mieux :zen:
Pour la question 4, qui est écrire
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
