P(X=k)=1/2^k et où je dois calculer l'espérance de X, mais je ne vois pas comment faire, j'ai:
mais, je ne vois pas comment simplifier ça...
Merci d'avance
Espérance
11 messages
- Page 1 sur 1
par murray » 04 Juin 2006, 20:57
bonjour,
ton problème revient en fait à calculer somme(k*x^k) (avec x =1/2 dans ton cas).
cette série entière est la dérivée (à peu de chose près ) de la série
somme(x^k)
Tu écris alors:
somme(x^k)= 1/(1-x).
puis tu dérives des deux côtés, et tu retrouveras ton expression.
ton problème revient en fait à calculer somme(k*x^k) (avec x =1/2 dans ton cas).
cette série entière est la dérivée (à peu de chose près ) de la série
somme(x^k)
Tu écris alors:
somme(x^k)= 1/(1-x).
puis tu dérives des deux côtés, et tu retrouveras ton expression.
par Zebulon » 05 Juin 2006, 06:01
Bonjour,
par ma méthode, je trouve E(X)=3. Murray, quel est votre résultat?
par ma méthode, je trouve E(X)=3. Murray, quel est votre résultat?
par Zebulon » 05 Juin 2006, 09:55
Voici comment j'ai fait :
Soit(x)=\sum_{k\ge0}{k\over{x^k}})
et =\sum_{k\ge0}x^{-k+1})
, alors par théorème de dérivation, =(\sum_{k\ge0}x^{-k+1})'=\sum_{k\ge0}(x^{-k+1})')
donc =\sum_{k\ge0}(x^{-k+1})'=\sum_{k\ge0}(-k+1)x^{-k}<br />\\=-\sum_{k\ge0}{k\over{x^k}}+\sum_{k\ge0}{1\over{x^k}}<br />\\=-E(X)(x)+{x\over{x-1}})
donc
(x)={x\over{x-1}}-S'(x))
.
=(\sum_{k\ge0}x^{-k+1})'<br />\\=(\sum_{k\ge1}{1\over{x^k}})'<br />\\=(\sum_{k\ge0}{1\over{x^k}}-1)'<br />\\=({x\over{x-1}}-1)'<br />\\=({1\over{x-1}})'<br />\\=-{1\over{(x-1)^2}})
donc
(x)={x\over{x-1}}+{1\over{(x-1)^2}}={{x^2-x+1}\over{(x-1)^2}})
donc(2)=3)
.
J'ai quand même peut-être fait une petite erreur...
Soit
donc
donc
donc
J'ai quand même peut-être fait une petite erreur...
par murray » 05 Juin 2006, 10:24
Ma méthode:
S(x)= sigma(x^k)= 1/(1-x)
S'(x)=sigma(kx^k-1)=1/(1-x)² (dérivation des 2 côtés)
et sigma(kx^k-1)=sigma((i+1)x^i)
D'ou sigma(i*x^i)= 1/(1-x)² -sigma(x^i)
sigma(i*x^i)= 1/(1-x)²- 1/(1-x)
on remplace ensuite x par 1/2
S(x)= sigma(x^k)= 1/(1-x)
S'(x)=sigma(kx^k-1)=1/(1-x)² (dérivation des 2 côtés)
et sigma(kx^k-1)=sigma((i+1)x^i)
D'ou sigma(i*x^i)= 1/(1-x)² -sigma(x^i)
sigma(i*x^i)= 1/(1-x)²- 1/(1-x)
on remplace ensuite x par 1/2
par Zebulon » 05 Juin 2006, 10:37
Oups! Ici c'est à partir de k=1, et moi j'ai fait à partir de k=0. C'est peut-être pour cela que nous n'avons pas les mêmes résultats. Je regarde.
par murray » 05 Juin 2006, 10:42
cela revient au même puisque k=0 compte pour zéro dans le calcul de l'espérance
par Zebulon » 05 Juin 2006, 10:47
Voilà la version corrigée et propre!
Soit et , alors par théorème de dérivation, donc =\sum_{k\ge0}(x^{-k+1})'=\sum_{k\ge0}(-k+1)x^{-k}<br />\\=-\sum_{k\ge0}{k\over{x^k}}+\sum_{k\ge0}{1\over{x^k}}<br />\\=-\sum_{k\ge1}{k\over{x^k}}-1+\sum_{k\ge0}{1\over{x^k}}<br />\\=-E(X)(x)+{x\over{x-1}}-1)
donc
(x)={x\over{x-1}}-S'(x)-1<br />\\=-S'(x)+{1\over{x-1}})
.
donc
(x)={1\over{x-1}}+{1\over{(x-1)^2}})
donc(2)=2)
.
Voilà ce qui clochait!
Soit
donc
donc
donc
Voilà ce qui clochait!
par Touriste » 05 Juin 2006, 10:57
Bonjour,
En fait, d'une façon générale, quand
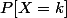
est un puissance comme ici (c'est ^k)
), le plus simple est d'utiliser la fonction génératrice et ses dérivées. Plus précisément,
=\sum_k P[X=k]s^k=\frac{s/2}{1-s/2})
(facile à calculer puisque c'est une série géométrique).
Ensuite,)
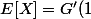et =G''(1)+G'(1)-G'(1)^2)
. Je passe bien sûr ici toutes les justifications qui sont normalement dans les cours, mais on oublie souvent d'utiliser cette fonction génératrice...
En fait, d'une façon générale, quand
Ensuite,
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :