Je souhaites démontrer:
Quelqu'un peut me donner une piste? Je suis parti de
Nombre complexe.
5 messages
- Page 1 sur 1
Nombre complexe.
par mitron » 05 Fév 2012, 12:22
Bonjour,
Je souhaites démontrer:^n = (\sqrt{2}exp^{\frac{3i\pi}{4}})^n)
.
Quelqu'un peut me donner une piste? Je suis parti de
et 
mais ça ne me donne aucun résultat.
Je souhaites démontrer:
Quelqu'un peut me donner une piste? Je suis parti de
par Le_chat » 05 Fév 2012, 12:28
Il faut écrire i-1 sous forme complexe.
Quel est le module de i-1? Un argument de i-1?
Quel est le module de i-1? Un argument de i-1?
par barbu23 » 05 Fév 2012, 15:50
Bonjour, :happy3:
Il faut reconvertir
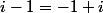
en forme trigonométrique d'abord ...
On a :
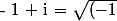^{2} + 1^{2} } \Big( \frac{-1}{\sqrt{ (-1)^{2} + 1^{2} }} + i \frac{1}{\sqrt{ (-1)^{2} + 1^{2} }} \Big) = \sqrt{2} \Big( - \frac{1}{\sqrt{2}} + i \frac{1}{\sqrt{2}} \Big) = \sqrt{2} \Big( - \frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2} \Big) = \sqrt{2} \Big( \cos ( \frac{3 \pi}{4} ) + i \sin ( \frac{3 \pi}{4} ) \Big) $)
Tu termines le calcul ... :happy3:
Cordialement. :happy3:
Il faut reconvertir
On a :
Tu termines le calcul ... :happy3:
Cordialement. :happy3:
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :