Convergence de suite

[MoRBT]

Bonjour,

Je n'arrive pas résoudre cet exo:

Soit une suite de réels supérieurs ou égaux à telle que, pour tout couple d’entiers , . On pose, pour tout au moins égal à , .
Montrer que la suite converge vers .


J'arrive à montrer que : , mais je ne sais pas comment démontrer que est une suite croissante
Je vous remercie par avance

[girdav]

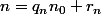
On a donc pour un fixé, on a en notant la division euclidienne et : donc , puis on prend la limite supérieure.

[MoRBT]

Merci de m'avoir répondu,

On a donc pour un fixé, on a en notant n=q_nn_0+r_n la division euclidienne donc , puis on prend la limite supérieure.

Comme ça, on a montré que la suite est bornée, mais pour qu'une suite converge il faut qu'elle soit à la fois bornée et "monotone" (croissante ou décroissante). Comment montrer que cette suite est croissante ?

Merci de m'expliquer

Je te remercie encore

[girdav]

Avec ça on a mieux puisque l'on démontre que pour tout , donc que et on a l'inégalité.

Je n'ai pas regardé si la suite est décroissante ou non (elle ne peut être croissante, à moins d'être constante).

[MoRBT]

Avec ça on a mieux puisque l'on démontre que pour tout , donc que et on a l'inégalité.

Je n'ai pas regardé si la suite est décroissante ou non (elle ne peut être croissante, à moins d'être constante).

Merci beaucoup girdav, je comprends maintenant.