Ensembles et applications
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
y6227
- Membre Naturel
- Messages: 26
- Enregistré le: 13 Nov 2011, 06:08
-
par y6227 » 31 Déc 2011, 02:41
Bonjour,
Voici la question d'un exercice :
Soient E et F deux ensembles et f une application E -> F.
Démontrer que :
)
 = f^{-1}(A) \cap f^{-1}(B))
Voici la correction du professeur:
}\Leftrightarrow f(x) \in {{A}\cap{B}})
 \in {A})
et
 \in {B})
})
et
})
}} \cap {{f^{-1}(B)}})
Pourtant en suivant le même raisonnement je peux montrer une autre égalité qui est :
)
 = f(A) \cap f(B))
qui est fausse si
Voici mon raisonnement en suivant celui du professeur :
}\Leftrightarrow f^{-1}(y) \in {{A}\cap{B}})
 \in {A})
et
 \in {B})
})
et
})
}} \cap {{f(B)}})
Où est donc l'erreur ?
Merci d'avance
-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
par alm » 31 Déc 2011, 03:30
Bonjour :
y6227 a écrit: Pourtant en suivant le même raisonnement je peux montrer une autre égalité qui est :
qui est fausse si
Voici mon raisonnement en suivant celui du professeur :
}\Leftrightarrow \red{ f^{-1}(y)} \in {{A}\cap{B}})
et
et
Où est donc l'erreur ?
Merci d'avance
l'erreur commence à la ligne ci-dessosus en rouge : tu as écris
)
qui n'a pas de sens ici.
Ce qui a un sens c'est
)
mais alors ce n'est pas un élément de
mais une partie de
Et si tu insistes de suivre ce mode de raisonnement, voici ce que, par exemple, tu peux dire :
 \Leftrightarrow f^{-1}\left(\{y}\right) \cap A \cap B \neq \emptyset)
Mais je te conseille de ne pas calquer la preuve du Prof (juste et belle mais pour l'image réciproque et pas l'image directe).
Tu peux plutôt dire : d'une part :
=y)
D'autre part :
 \cap f(B) \Leftrightarrow y \in f(A) \quad \text{et} \quad y \in f(B) \Leftrightarrow \exists(a,b) \in A \times B \quad y=f(a)=f(b))
et tu vois qu'on a besoin que
soit injective pour avoir
!
Moralité si
est injective on a bien
=f(A) \cap f(B))
pour toutes parties
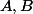
de
Sinon pas forcément ....
PS: la propriété :
 \quad \quad (\forall(A,B) \in ({\mathscr P}(E))^2 \quad f(A \cap B)=f(A) \cap f(B))
caractérise le fait que
est injective.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
