Je fais appel aux grands esprits pour m'aider à résoudre ce problème : :help: :help: :help:
Un jeu consisite à tirer simultanément 3boules d'une urne contenant 6blanches et 4rouges.On suppose que tous les tirages sont équiprobables.
-->Si les 3boules tirées sont rouges le joueur gagne 100
-->Si exactement 2boules tirées sont rouges: 15
-->Si 1seule boule tirée est rouge: 4
-->Dans tous les autres cas il ne gagne rien.
Soit X la variable aléatoire qui prend pour valeur le gain en du joueur.
1/-Déterminer la loi de probas. de X
2/-Pour 1jeu la mise est de 10.Le jeu est-il favorable au joueur, cad l'espérance mathématique de X est'elle strictement supérieure à 10.
3/-Pour l'organisateur le jeu n'est pas rentable donc il envisage 2solutions:
a) Soit augmenter la mise de 1
b) Soit baisser chaque gain de 1
Quelle est la solution la plus rentable pour l'organisateur ???
P.S.: Pour info c'est le sujet de nouvelle-calédonie de septembre 2002 !!! Voila à très vite j'espère et merci de m'aider... :++: :++: :++: :++: :++:
Bonjour à tous pb de probas !!!
5 messages
- Page 1 sur 1
Re,
1)La loi de probabilité de X:
les valeurs prises par X sont 0,4,15,100
l'urne contient 10 boules on en tire 3 simultanement il y a donc façons de le faire
façons de le faire
donc on va calcler les differentes probabilités de la variable aleatoire X
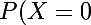}) c'est la probabilite de tirer 3 boules blanches parmis les 6 que contient l'urne il y a
c'est la probabilite de tirer 3 boules blanches parmis les 6 que contient l'urne il y a  façons de le faire donc
façons de le faire donc
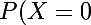}=\frac{C_6^{3}}{C_{10}^{3}}=\frac{20}{120}=\frac{1}{6})
essiaes de faire les autres sur le même modèle
2) formule pour calculer l'eperance:
}=\sum_{i=1}^{n}x_iP(X=x_i))
il faut que E(X)>10
3) il faut que tu recalcules l'esperance mathematiques avec les nouveau chiffre pour savoir la solution qui est la plus rentable
1)La loi de probabilité de X:
les valeurs prises par X sont 0,4,15,100
l'urne contient 10 boules on en tire 3 simultanement il y a donc
donc on va calcler les differentes probabilités de la variable aleatoire X
essiaes de faire les autres sur le même modèle
2) formule pour calculer l'eperance:
il faut que E(X)>10
3) il faut que tu recalcules l'esperance mathematiques avec les nouveau chiffre pour savoir la solution qui est la plus rentable
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
