Calcul de somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 19 Nov 2011, 05:28
par mehdi-128 » 19 Nov 2011, 05:28
Bonjour,
comment calculer :
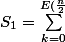} \, \binom{n}{2k} \,)
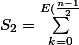} \, \binom{n}{2k+1} \,)
C'est la partie entière qui me gêne sinon j'aurais utilisé le Binôme de Newton ...
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 19 Nov 2011, 11:00
par Maxmau » 19 Nov 2011, 11:00
Bj
distingue les cas n pair , n impair
-
le_passager
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Nov 2011, 11:03
-
 par le_passager » 19 Nov 2011, 11:15
par le_passager » 19 Nov 2011, 11:15
mehdi-128 a écrit:Bonjour,
comment calculer :
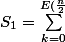} \, \binom{n}{2k} \,)
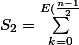} \, \binom{n}{2k+1} \,)
C'est la partie entière qui me gêne sinon j'aurais utilisé le Binôme de Newton ...
fais (1-1)a la puissance n. tu devrais trouver s1-s2. ensuite tu calcules s1+s2.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 19 Nov 2011, 12:00
par mehdi-128 » 19 Nov 2011, 12:00
Maxmau a écrit:Bj
distingue les cas n pair , n impair
Bah si n est pair :
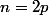
=E(\frac{2p}{2})=p)
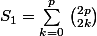
Et là je bloque.
Dans le Binôme de Newton, c'est du k pas du 2k ...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Nov 2011, 12:14
par Doraki » 19 Nov 2011, 12:14
Mais enfin, t'as fait quasiment le même problème la semaine dernière
http://www.maths-forum.com/binome-newton-118831.phpAvec la méthode donnée par l'énoncé (contrairement à ici, ok), et avec le MEME obstacle
J'arrive pas à utiliser la formule du Binôme à cause des 3k, 3k+1 et 3k+2. Dans le cours c'est k
Dans le Binôme de Newton, c'est du k pas du 2k ...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 19 Nov 2011, 12:25
par mehdi-128 » 19 Nov 2011, 12:25
Oui mais c'était un DM guidé c'était différent.
Là c'est une question seule.
-
le_passager
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Nov 2011, 11:03
-
 par le_passager » 19 Nov 2011, 12:46
par le_passager » 19 Nov 2011, 12:46
mehdi-128 a écrit:Oui mais c'était un DM guidé c'était différent.
Là c'est une question seule.
la DM guidee te permet de calculer S1+S2 et (1-1)^n te permet de calculer S1-S2. tu obtiendras alors un systeme d'equations d'inconnues S1 et S2.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 19 Nov 2011, 12:51
par mehdi-128 » 19 Nov 2011, 12:51
le_passager a écrit:la DM guidee te permet de calculer S1+S2 et (1-1)^n te permet de calculer S1-S2. tu obtiendras alors un systeme d'equations d'inconnues S1 et S2.
Oui mais la les 2 questions sont indépendantes.
Un exo demande de calculer S1, un autre de calculer S2.
Donc je pense qu'il faut faire sans.
-
le_passager
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Nov 2011, 11:03
-
 par le_passager » 19 Nov 2011, 13:40
par le_passager » 19 Nov 2011, 13:40
mehdi-128 a écrit:Oui mais la les 2 questions sont indépendantes.
Un exo demande de calculer S1, un autre de calculer S2.
Donc je pense qu'il faut faire sans.
cette methode reste valable meme si on ne demande que S1. ici on a la chance qu'on nous ait mis S2.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 19 Nov 2011, 14:11
par mehdi-128 » 19 Nov 2011, 14:11
le_passager a écrit:cette methode reste valable meme si on ne demande que S1. ici on a la chance qu'on nous ait mis S2.
Ok mais je vois pas le rapport entre (1-1)^n et les sommes
-
le_passager
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Nov 2011, 11:03
-
 par le_passager » 19 Nov 2011, 14:22
par le_passager » 19 Nov 2011, 14:22
mehdi-128 a écrit:Ok mais je vois pas le rapport entre (1-1)^n et les sommes
je vois.
calcules (1+(-1))^n en utilisant la formule du binome. la somme des termes dont la puissance de (-1) est impaire donne quoi? meme question pour les puissances paires.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités