Trigo réciproque (MPSI)

[pia-ju]

Bonjour!!
N'étant pas une lumière et pourtant en MPSI (malin n'est-ce pas..), et ayant un prof de maths qui à "monsieur je n'ai pas compris ça" répond "ben faut réfléchir!", j'écris pour la première (et certainement pas la dernière!) fois sur ce type de forum afin de soliciter votre aide

J'ai eu une khole tout à l'heure avec entre autres cet exercice (ils sont à refaire pour le lendemain de la khole) :

-Resoudre : 2arcsin(x)=arcsin(2xV(1-x²)) (je prends V en racine carrée..)
déjà en khole j'étais arrivée à la conclusion : cos(arcsin(x))=V(1-x²)
Premièrement : je suis bloquée à cette étape, ne vois pas du tout par où ni par quoi il faut aller et à laquelle le prof de khole m'a dit de passer à la suite donc pas terminé mais à terminer pour demain

Deuxièmement, avant la toute première étape, pour laquelle mon prof tout à l'heure m'a dit (ce que mon kholeur ne m'a pas dit) "il faut prouver que cette égalité soit vraie"..?????? (eh oui, le fameux "il faut réfléchir"^^)


Pourriez-vous me donner quelques conseils, je ne cherche pas de réponses mais des indices pour continuer.. Je n'ai absolument aucun scientifique dans ma famille pour m'aider et assez de ces profs qui m'envoient "ballader"

[Bony]

Posons x = sin(t)

2*arcsin(x) = ...

2*x*sqrt(1-x²) = 2*sin(t) * cos(t) = ...

[el niala]

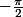
arcsin est défini sur [-1,+1] et renvoie une valeur entre et

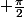
x=0 est solution triviale, et pour x0 on arrive simplement à la relation que tu as trouvée (en prenant le sinus de chaque membre)
et comme sur l'intervalle de définition, c'est une identité, tu as dû la voir en cours ou en TD non ?

@ Bony, mieux vaudrait t=sin(x) vu les notations de l'énoncé mais il me semble que ça il a su faire

[pia-ju]

Tout d'abord merci :-)
Ensuite..

2*arcsin(x) = 2t
2*x*sqrt(1-x²) = 2*sin(t) * cos(t) = ???

sqrt(1-sin²(t))=cos(t)????

ou j'ai loupé quelque chose..

[pia-ju]

Et ba nan ELLE a pas sû faire..
Vous ai dit je suis pas une lumière ><"
Pour le domaine de définition oui je le connais, cela fait partie du cours mais je ne comprends pas comment appliquer cela à l'exo.
Je vais me reconcentrer sur le reste de la réponse je n'ai pas tout saisi..
(merci aussi^^)

[el niala]

x=0 solution triviale ou



élève au carré



qui s'écrit plus simplement

[Bony]

2*sin(t)*cos(t) = sin(2*t).

Il est important de bien connaître ses relations trigonométriques, spécialement dans le cadre des fonctions usuelles

[pia-ju]

Merci beaucoup!
Et merci de votre solidarité d'hier soir, malheuresement ma connexion internet n'a pas voulu l'être autant, solidaire :'(
En bref, j'ai rendu mon cahier de khole sans rien de plus que ce que j'avais déjà trouvé, mon prof me dira sans doute demain que je n'ai rien foutu et même pas essayé :p mais ça je vais finir par m'y habituer..
C'est l'"élevation" ("l'élevage"?) au carré qui ne m'était pas venue à l'esprit à la fin.. je connais mes formules de trigo mais ai du mal à voir quand je peux les appliquer. C'était donc ça..

Sinon pour la première question, à savoir prouver que la première égalité est vraie (au passage je n'ai pas vu le terme "trivial" en cours mais crois comprendre de quoi vous parlez), une fille de ma classe m'a dit ce matin qu'il fallait déjà poser x appartient à ]-1;1[ (pour 2arcsin(x)) et 2xsqrt(1-x²) appartient à ]-1;1[ (pour arcsin(2xsqrt(1-x²)) )Est-ce vrai? Cela suffit-il à dire que l'égalité peut exister pour ensuite embrayer sur le calcul?
Dans le cas où oui, j'aurais tendance à faire :


-1 la raison pour laquelle vous dites que "x=0 est solution triviale"..?

Est-ce bien cela?




Par contre après l'élév**** au carré je me retrouve avec x=x au bout du compte..
C'est là qu'il faut faire intervenir la relation sin(2a)=2cos(a)sin(a)..????
Comprends pas bien

[el niala]

bonsoir
non, ce n'est pas ça

- une solution triviale est une solution évidente
regarde la 4ème ligne de mon post d'hier à 21h22
x est en facteur des 2 membres de l'égalité, si x=0 celle-ci est vérifiée non ?
et alors tu peux continuer en divisant par x non nul

- pour moi le domaine de définition de la fonction arcsinus c'est [-1, +1] et non ]-1, +1[, sinon tu "oublies" et

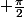
- attention !
[quote]-1 0x²<+1

quant à la démonstration, il est très élégant de partir de la dernière ligne que j'ai écrite pour retrouver l'égalité de l'énoncé

ne te décourage pas, l'année est longue, il est normal que tu patauges un peu au début, surtout si tu n'as eu la chance d'être dans une TS "préparatoire"

[pia-ju]

OK pour l'égalité large, j'y ai pensé après avoir posté ^^'
Compris pour la solution triviale aussi.
En revanche, "résoudre" c'est exprimer x en fonction de quelque chose non?
Je ne comprends pas non plus ça :
-1 0Je me suis peut-être embrouillée en voulant élever au carré -1 et 1 au lieu de multiplier par x de chaque côté (mais ça revient au même non?)
Donc pourquoi 0??

[el niala]

pourquoi 0 ?

-1 0 |x|< +1 non ? et donc 0² |x|^2< (+1)² non ?

et donc le résultat

fais attention quand tu élèves au carré une inégalité où apparaît un signe "-"

et pour "résoudre" c'est trouver toutes les solutions

[pia-ju]

Je ne comprends pas trop l'intégration d'une valeur absolue mais ça peut venir..
Oui et donc je ne comprends pas d'où sin²+cos²=1 peut m'aider, en retournant ça dans tous les sens je me retrouve avec x=x :mur:

[el niala]

on reprend calmement :

- pour ce que tu appelles abusivement une "intégration"

tu pars de la double inégalité -1<x<+1
tu élèves au carré... sans vergogne, oubliant ce que tu as appris au lycée
"quand on multiplie les membres d'une inégalité par un réel négatif on change le sens de l'inégalité"
or que fais-tu quand tu élèves -1 au carré ? tu multiplies par un réel négatif, sans compter que la fonction carré n'est pas monotone !

pour la résolution de l'équation

si tu pars de l'égalité cos²t+sin²t=1
tu dois aboutir (en suivant la démarche de mon post d'hier à 21h22 dans le sens opposé) à l'équation de ton énoncé
ce qui signifie que cette dernière est vérifiée quel que soit x compris entre -1 et +1 (domaine de définition de la fonction arcsinus)

[pia-ju]

D'accord je crois que j'ai saisi le principe.. merci beaucoup
Je ferai ça dès que j'aurai récupéré mon cahier de khole c'est à dire demain (on doit le donner au prof qui nous le rend et ainsi de suite jusqu'à ce que tout soit parfais..)
Bonne soirée :-)