Nombres complexes(2)

[geo2math]

Je ne sais pas comment faire l'ex suivant:
on considère z^4+(1-2i)z^3+pz^2-(1+2i)z+q=0
déterminer p et q de telle manière que cette équation posssède un racine double en z=i.Ensuite pour ces valeurs de p et q calculer les autres racines complexes de l'équation.
Merci d'avance pour votre aide

[SaintAmand]

Je ne sais pas comment faire l'ex suivant:
on considère z^4+(1-2i)z^3+pz^2-(1+2i)z+q=0
déterminer p et q de telle manière que cette équation posssède un racine double en z=i.Ensuite pour ces valeurs de p et q calculer les autres racines complexes de l'équation.

Soit P(X) est un polynôme. Si a est une racine, alors il existe un polynôme Q(X) et un entier positif n tel que . n est la multiplicité de la racine (pour une racine double, n=2).

[busard_des_roseaux]

[Black Jack]

Autrement :

(z - i)² = z² - 2iz - 1

z^4+(1-2i)z^3+pz^2-(1+2i)z+q est donc divisible par (z²-2iz-1)

On fait la division euclidienne de [z^4+(1-2i)z^3+pz^2-(1+2i)z+q] par (z²-2iz-1)

Et on exprime que le reste de cette division (que l'on trouve égal à [(-4+2ip).z + (q+p+1+2i)] doit être nul pour tout z.

:zen:

[Anonyme]

Bonjour
Une autre méthode est d'appliquer le conseil de busard_des_roseaux :
si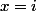 est racine double de ce polynôme
alors on a :

Cela va te donner un système de 2 équations à 2 inconnues en p et q

Après avoir trouvé les valeurs de p et q ,
tu peux appliquer le conseil de Black Jack, en faisant une division euclidienne pour trouver Q(z) tel que


ps)
Tu peux aussi utiliser le fait que
et trouver a,b et c en utilisant la méthode "d'identification" des coefficients d'un polynôme (unicité de son expression)

[Black Jack]

Bonjour
Une autre méthode est d'appliquer le conseil de busard_des_roseaux :
si est racine double de ce polynôme
alors on a :

Cela va te donner un système de 2 équations à 2 inconnues en p et q

Après avoir trouvé les valeurs de p et q ,
tu peux appliquer le conseil de Black Jack, en faisant une division euclidienne pour trouver Q(z) tel que


ps)
Tu peux aussi utiliser le fait que
et trouver a,b et c en utilisant la méthode "d'identification" des coefficients d'un polynôme (unicité de son expression)

Pourquoi "Après avoir trouvé les valeurs de p et q , tu peux appliquer le conseil de Black Jack"...

Si on suit ma méthode, on trouve directement p et q en exprimant que le reste de la division est nul pour tout x ...
Mais la division euclidienne ayant été faite, on a aussi trouvé le quotient (qui est z² + z + (p+1+2i)) ... et comme on connait p, on a directement l'expression de Q(x)

:zen:

[Anonyme]

OUI Black Jack
Sauf que le division euclidienne de 2 polynômes est peut être "une notion compliquée" pour certains lycéens qui dès qu'il faut faire se précipitent sur leur calculatrice....

C'était le propo de mon message précédent mais , tu as raison : ta méthode est une des méthodes qu'un lycéen peut comprendre et utiliser pour résoudre cet exercice (s'il connait et se souvient de ce qu'est une "division Euclidienne"....et également une "division Euclidienne de 2 polynômes")