Solution d'un complexe

[dodi27930]

Bonsoir j'aimerais un coup de main pour résoudre un exo.

Voici l'énoncé :
On considère l'équation : (E) : (z-(1+i))(z barre-(1-i))=4
(a) 1. Déterminer tous les réels qui sont solutions de (E).
2. Déterminer tous les imaginaires purs qui sont solutions de (E).
(b) 1. On pose : z=x+iy avec x appartenant à R et y appartenant à R.
Quelle est la condition nécessaire et suffisante à laquelle doivent satisfaire x et y pour que z soit solution de (E).
2. En déduire l'ensemble des points M d'affixe z vérifiant (E). Retrouver les résultats obtenus en (a).

Pour la (a) J'ai commencé à développer mais je suis bloquer aprés. Est ce qu'il faut faire par identification pour trouver les réponses ?
Et pour la (b), je n'ai pas compris la question.

Pouvez-vous m'aider s'il vous plait. Merci d'avance.

[Vahngal]

Bonsoir j'aimerais un coup de main pour résoudre un exo.

Voici l'énoncé :
On considère l'équation : (E) : (z-(1+i))(z barre-(1-i))=4
(a) 1. Déterminer tous les réels qui sont solutions de (E).
2. Déterminer tous les imaginaires purs qui sont solutions de (E).
(b) 1. On pose : z=x+iy avec x appartenant à R et y appartenant à R.
Quelle est la condition nécessaire et suffisante à laquelle doivent satisfaire x et y pour que z soit solution de (E).
2. En déduire l'ensemble des points M d'affixe z vérifiant (E). Retrouver les résultats obtenus en (a).

Pour la (a) J'ai commencé à développer mais je suis bloquer aprés. Est ce qu'il faut faire par identification pour trouver les réponses ?
Et pour la (b), je n'ai pas compris la question.

Pouvez-vous m'aider s'il vous plait. Merci d'avance.

Il faut remarquer que (zbarre-(1-i)) est le complexe conjugué de (z-(1+i))

Que sait tu sur le produit d'un complexe avec son conjugué ?
Appliquer à z=x appartenant aux nombres réels. ( tu obtiens 2 solutions )

[dodi27930]

je sais z*z barre = module de z au carré. Mais je n'ai pas compris la suite. Pouvez vous détaillé s'il vous plait. Merci d'avance.

donc z²=2 c'est sa ?

[Vahngal]

1. Ensemble des réels solutions de (E)

Tu poses z=x avec x appartenant à R et tu calcules le module...

[dodi27930]

module de (x-(1+i)²) au carré = 4
racine de (x²+(-1)²+(-1)²) le tout au carré =4
x²+1+1=4
x²=2

donc x= - racine de 2 ou x = racine de 2

Est ce que ma démarche est bonne ?

Merci.

[Vahngal]

module de (x-(1+i)²) au carré = 4
racine de (x²+(-1)²+(-1)²) le tout au carré =4
x²+1+1=4
x²=2

donc x= - racine de 2 ou x = racine de 2

Est ce que ma démarche est bonne ?

Merci.

Non car n'est pas égal à

Calcules tout d'abord avec x réel

[dodi27930]

module de (x-(1+i)) = racine de (x²+1²+1²) = racine de (x²+2)

Est ce que c'est ca ?

Merci

[Vahngal]

module de (x-(1+i)) = racine de (x²+1²+1²) = racine de (x²+2)

Est ce que c'est ca ?

Merci

Non il faut d'abord que tu "sépares" partie réelle et partie imaginaire.

[dodi27930]

module de (x-(1+i)) = module de (x-1-i) = module de ((x-1) -i)
= racine de [(x-1)²+1²]
= racine de [x²-2*x*1+1²+1²]
= racine de [x²-2x+2]

[Vahngal]

D'où x²-2x+2 = 4

Donc x = ?

[dodi27930]

x²-2x+2=4
x²-2x-2=0

x1= (2+ racine de 12) / 2 et x2= (2- racine de 12) / 2

x1= 1+ racine de 3 et x2= 1- racine de 3

[Vahngal]

Je vais me coucher.
Si z est imaginaire pur, poser z=iy et tu recommences

Tu te rendras compte que tu obtiens 2 solutions y1 et y2 tels que x1=y1 et x2=y2.

Pourquoi ?
En posant zo = 1+i, tu remarques que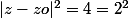 est l"équation d'un cercle de centre d'affixe zo dans le plan complexe et de rayon R= 2

Si tu ne le vois pas, en posant z=x+iy et zo=xo+iyo tu obtiens

Je ne réponds pas aux questions dans l'ordre, mais en fait tout est dit... Je te laisse le soin de reformuler pour faire une présentation propre.

Bonne nuit

[dodi27930]

Merci Bonne nuit