Continuité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Déc 2010, 15:51
par Nightmare » 03 Déc 2010, 15:51
laura1205 a écrit:
par la dérivée que vous m'avez donné, j'obtiens donc:
9*(x-3)-(9x-15)*1 / (x-3)²
soit -42 au numérateur et en dessous comment faire?
Ok c'est presque bon, on obtient -27 + 15 (et non -15 ) au numérateur soit -12, le dénominateur tu peux le laisser comme cela, il est très bien ainsi !
Donc la dérivée du deuxième facteur est
^{2}})
et celle du premier facteur (x-3) est -3. Tu peux alors appliquer pour terminer la formule de dérivée d'un produit que je t'ai donnée.
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 15:58
par laura1205 » 03 Déc 2010, 15:58
euh pourquoi pour (x-3) c'est égal à 3 pour la dérivé?
j'aurais dis 1 moi ...
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 15:59
par laura1205 » 03 Déc 2010, 15:59
-3 pardon ..
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 16:20
par laura1205 » 03 Déc 2010, 16:20
alors la dérivée de h(x)= (x-3)(x²-(3(3x-5))) / (x-3)
est égale à -3*2x-(-12) / (x-3)²
oui ou non?
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 03 Déc 2010, 18:31
par bentaarito » 03 Déc 2010, 18:31
Nightmare a écrit:Ok c'est presque bon, on obtient -27 + 15 (et non -15 ) au numérateur soit -12, le dénominateur tu peux le laisser comme cela, il est très bien ainsi !
Donc la dérivée du deuxième facteur est
^{2}})
et celle du premier facteur (x-3) est -3. Tu peux alors appliquer pour terminer la formule de dérivée d'un produit que je t'ai donnée.
oui j'avoue c'est 1. Nightmare a du faire une faute de frappe ( ça arrive à tt le monde!) :lol3:
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 03 Déc 2010, 18:34
par bentaarito » 03 Déc 2010, 18:34
laura1205 a écrit:alors la dérivée de h(x)= (x-3)(x²-(3(3x-5))) / (x-3)
est égale à -3*2x-(-12) / (x-3)²
oui ou non?
Non , c'est pas bon.t'as tout mélangé!!
Rappel : (uv)'=u'v+uv' et (x-3)'=1 et le second facteur Nightmare t'en as donné la dérivée
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 18:36
par laura1205 » 03 Déc 2010, 18:36
comment fait-on pour trouver le nombre de solutions de h(x)=0 sur [0;2] ??
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Déc 2010, 18:40
par Jimm15 » 03 Déc 2010, 18:40
Bonsoir,
La méthode la plus simple et la plus sûre est de saider du tableau des variations de la fonction
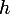
.
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 19:14
par laura1205 » 03 Déc 2010, 19:14
est-ce normal que je trouve aucune solution en faisant le tableau de variation de h ?
grrr
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Déc 2010, 20:35
par Nightmare » 03 Déc 2010, 20:35
bentaarito a écrit:oui j'avoue c'est 1. Nightmare a du faire une faute de frappe ( ça arrive à tt le monde!) :lol3:
Souvent à moi :happy3:
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 20:53
par laura1205 » 03 Déc 2010, 20:53
rien de grave, vous m'avez été d'un très grand aide.
mais une dernière question, comment fait ton pour trouver le nombre de solution de h(x)=0 sur l'intervalle [0;2]
j'ai essayé avec un tableau de variation, et je trouve aucune solution, ce qui doit pas etre la bonne méthode, grr
pouvez vous m'aidez svp
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Déc 2010, 21:15
par Jimm15 » 03 Déc 2010, 21:15
Bonsoir,
Pour la dérivée de
=x^2-\frac{3(3x-5)}{x-3})
, jobtiens
=2x-\frac{-12}{(x-3)^2}=2x+\frac{12}{(x-3)^2})
.
Ai-je raison ou ai-je fait une erreur ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Déc 2010, 21:24
par Nightmare » 03 Déc 2010, 21:24
Tu as raison, c'est bien f(x)-g(x) et non f(x)+g(x) qu'on considérait !
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 21:26
par laura1205 » 03 Déc 2010, 21:26
oui j'ai trouvé la meme chose, merci !
mais comment faire pour déterminer le nombre de solutions (h)=0 sur [0;2] ??
:cry:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 03 Déc 2010, 21:29
par Sylviel » 03 Déc 2010, 21:29
As tu fait le tableau de variations de h ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
laura1205
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Déc 2010, 16:03
-
 par laura1205 » 03 Déc 2010, 21:37
par laura1205 » 03 Déc 2010, 21:37
ui j'ai fait le tableau de variation, et dans ma courbe, sa coupe pas 0, ce qui est pas normale.
je dois faire une erreur, pouvez vous m'éclaircir sur la méthode svp
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 03 Déc 2010, 21:40
par Sylviel » 03 Déc 2010, 21:40
Ben donne nous déjà le tableau de variation et comment tu l'as obtenu ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Déc 2010, 21:43
par Jimm15 » 03 Déc 2010, 21:43
Quelle expression finale de

obtiens-tu ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2010, 21:46
par Ben314 » 03 Déc 2010, 21:46
Salut,
Juste une toute petite remarque :
Il me semble que, pour dériver
=(x - 3) \times \left(x^{2}-\frac{3(3x-5)}{x-3}\right))
, il aurait été un peu plus simple de commencer par dire que
=(x - 3)x^{2}-3(3x-5)=x^3-3x^2-9x+15)
....
Bon, d'accord, j'arrive un peu "aprés la pluie"...

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Déc 2010, 21:51
par Jimm15 » 03 Déc 2010, 21:51
Ben314 a écrit:Salut,
Juste une toute petite remarque :
Il me semble que, pour dériver
=(x - 3) \times \left(x^{2}-\frac{3(3x-5)}{x-3}\right))
, il aurait été un peu plus simple de commencer par dire que
=(x - 3)x^{2}-3(3x-5)=x^3-3x^2-9x+15)
....
Bon, d'accord, j'arrive un peu "aprés la pluie"...

Petite mais très bonne remarque.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
