Démonstration : Continuité !
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par Al-khawarizmi » 21 Nov 2010, 12:32
par Al-khawarizmi » 21 Nov 2010, 12:32
Salut !
Soient f et g deux fonctions définies de

telles que :
f et g sont continues sur [0;1] Et
 = [0;1])
Démontrer que :
=g(x_0))
Merci .

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Nov 2010, 12:45
par Ben314 » 21 Nov 2010, 12:45
Salut
Niveau Lycée, c'est pas totalement évident...
Comme
 = [0;1])
, il existe en particulier
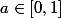
tel que
=0)
et aussi

tel que
=1)
.
Que peut tu dire du signe de
-g(a))
? et de celui de
-g(b))
?
Or la fonction
-g(x))
est ... donc vérifie le théorème des ... et donc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par Al-khawarizmi » 21 Nov 2010, 13:05
par Al-khawarizmi » 21 Nov 2010, 13:05
Ben314 a écrit:Salut
Niveau Lycée, c'est pas totalement évident...
Comme
 = [0;1])
, il existe en particulier
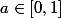
tel que
=0)
et aussi

tel que
=1)
.
Que peut tu dire du signe de
-g(a))
? et de celui de
-g(b))
?
Or la fonction
-g(x))
est ... donc vérifie le théorème des ... et donc...
Oui je vois. On va appliquer alors Le théorème des valeurs intermédiaires !
Merci .
-
mathlegend
- Membre Relatif
- Messages: 133
- Enregistré le: 13 Nov 2010, 17:40
-
 par mathlegend » 21 Nov 2010, 13:11
par mathlegend » 21 Nov 2010, 13:11
:ptdr: :ptdr: \ :lol3: :ptdr:;)
 par Al-khawarizmi » 21 Nov 2010, 13:53
par Al-khawarizmi » 21 Nov 2010, 13:53
mathlegend a écrit::ptdr: :ptdr: \ :lol3: :ptdr:;)
ça te fait tellement rire ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
, il existe en particulier
tel que
et aussi
tel que
.
? et de celui de
?
est ... donc vérifie le théorème des ... et donc...