Nombres Complexes DM

[jou_71]

Bonjour a tous,

J'ai un DM a rendre bientot et je ne trouve pas certaines questions

On considère dans le plan complexe les points O d'affixe 0, A d'affixe 1 et B d'affixe -1.
A tout point M d'affixe z différent de 1, on associe le point M' dont l'affixe z' est tel que l'on ait: z'=(z-1)/(1-zconjugué).
on a aussi : z'conjugué=1/z'
QUESTION 3: prouver que (z'-1)/(z-1) est réel.

Merci d'avance pour vos réponses.

[johnjohnjohn]

Bonjour a tous,

J'ai un DM a rendre bientot et je ne trouve pas certaines questions

On considère dans le plan complexe les points O d'affixe 0, A d'affixe 1 et B d'affixe -1.
A tout point M d'affixe z différent de 1, on associe le point M' dont l'affixe z' est tel que l'on ait: z'=(z-1)/(1-zconjugué).
on a aussi : z'conjugué=1/z'
QUESTION 3: prouver que (z'-1)/(z-1) est réel.

Merci d'avance pour vos réponses.

ça peut se démontrer directement par un calcul bourrin et simple. Sinon ça doit pouvoir se déduire des deux précédentes questions que tu n'as pas pas pris la peine de poster.

[jou_71]

Non les deux questions d'avant ne servent pas a cette question, juste ce que j'ai mi peut la résoudre, comment faire?

[Ericovitchi]

Tu as juste à écrire (z'-1)/(z-1) et remplacer z'
tu vas trouver que c'est égal qu'à des choses réelles car il ne restera plus que des termes en
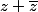
qui est réel car égal à 2 fois la partie réelle de z
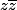
qui est réel car c'est le module de z au carré

[jou_71]

J'ai bien compri merci mais comme résultat je trouve (z-z'z)/(z'-z'z) et pas des termes comme vous le dites ...

[jou_71]

Ah si c'est bon j'ai trouvé un résultat avec les bons termes merci.

J'ai aussi une question qui est : à l'aide des point O,A,M et M' interpréter géométriquement les propriétés établies avant qui sont: (z'-1)/(z-1) réel et |z'|=1
Comment faire parce que la je n'ai aucune idée ...

[Ericovitchi]

non, j'ai dit qu'il fallait remplacer z' par (z-1)/(1-zconjugué)


Voilà, tout est réel là-dedans

[Ericovitchi]

z'-1 est l'affixe du vecteur AM' et est l'affixe du vecteur formé par le symétrique de M par rapport à l'axe des x (appelons le P) et A. La relation montre que l'argument de AM' - l'argument de PA = 0 donc PA et M' sont alignés et comme M' est sur le cercle de rayon 1 c'est l'intersection de PA avec le cercle.

[jou_71]

Je ne comprend pas tout comment trouver argument de AM' - argument de PA=0 ?? Et géométriquement je ne peux pas placer le point M ni le point M' donc je n'arrive pas à faire une figure...

[Ericovitchi]

L'argument d'un quotient est la différence des arguments

[jou_71]

C'est bon pour cette question, merci :).

Y m'en reste une seule : Donner une construction géométrique élementaire du point M' connaissant le point M.

Comment faire ?

[Ericovitchi]

je te l'ai mise dans mon avant dernier post, ça ne te convient pas ?

[jou_71]

Disons que je ne comprend pas tout, du coup je n'arrive a faire une figure avec ce qui y a d'écrit..

[Ericovitchi]

La construction c'est de prendre le symétrique P de M par rapport à l'axe des x, de tracer la droite AP et de prendre l'intersection (autre que A) avec le cercle de rayon 1 centré à l'origine et ça donne M'.