Expression de f(x) en fonction de sa dérivée

[ze zoune]

Bonjour à tous,

Je bloque sur une question, pourriez vous m'aider à démarrer ?

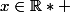
On a pour tout la fonction f tq . On suppose que f convient. Il s'agit d'exprimer f(x) à l'aide de f' pour tout x strictement positif.
J'avais pensé pouvoir utiliser les fonctions ln ou exp, mais rien de bien concluant !

Merci de m'aider !

[arnaud32]

je te conseille de regarder ce que verifie f''(x)

[ze zoune]

Ok donc je trouve f''(x)=f(x), maintenant que dire lorsqu'une fonction est égale à sa dérivée seconde ?

[arnaud32]

tu es sure?

[qshanshan]

oui dans le bios tout est bien paramétré, TN Requin|Tn Requin|Air Max 90|Tn|Tn Requinet comme je le disais dans le premier message, j'ai testé cette imprimante sur la même carte mère, et là ça fonctionne très bien, c'est ce qui me fait dire qu'il doit y avoir un problème avec ma carte mère.

[ze zoune]

On a f'(x)=f(1/x), donc f''(x)=f'(1/x)=f(x). Non ?

[arnaud32]

f''(x)=(1/x)'f'(1/x)=-1/x²f'(1/x)=-1/x²f(x)

[ze zoune]

Ah effectivement ce n'est pas pareil. Et si j'ai bien compris la question, il n'est pas nécessaire de faire disparaître f' ou f" dans l'expression ?

[arnaud32]

si tu veux juste f en fonction de f'
ou

[ze zoune]

Ok merci beaucoup, je vais essayer d'avancer ! :)