Suite en terminale S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 11:38
par alex-blade2 » 19 Oct 2010, 11:38
Bonjour j'ai un exercice que je n'arrive pas à résoudre je vous donne l'énoncé :
Soit la suite (Un) définie sur IN* par :
| U1 = -1
| Un+1 =
}Un+\frac{3(n+2)}{2(n+1)})
Il m'est demandé d'étudier le sens de variation de cette suite, mais comment faire normalement je dois faire Un+1 - Un mais ici je ne sais pas quoi prendre pour Un, quelqu'un pourrait m'aider ?
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 12:24
par alex-blade2 » 19 Oct 2010, 12:24
S'il vou plaît j'ai vraiment besoin d'aide je suis bloqué depuis au moins 2 jours sur cet exercice.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Oct 2010, 13:08
par Ericovitchi » 19 Oct 2010, 13:08
Oui il faut faire Un+1-Un
Mets la sous la forme
}{2(n+1)}(3-u_n))
Au début

est inférieur à 3, montres qu'elle le reste et que donc

est toujours positif et que un est donc croissante (et majorée par 3).
Elle converge vers 3 d'ailleurs en fait.
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 13:37
par alex-blade2 » 19 Oct 2010, 13:37
Dans une première question il m'était demandé de prouver par récurrence que (

) était majorée par 3 donc j'ai bien ce résultat là.
Mais comment trouvez vous cette forme pour
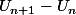
?
Si je fais
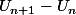
après le mets au même dénominateur, je développe réduits, j'obtiens :
})
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 13:59
par alex-blade2 » 19 Oct 2010, 13:59
Pourquoi il y a un -1 dans la première étape du calcul ?
Et n n'est pas égale a n -2n -2 ? Je ne comprends pas ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Oct 2010, 14:15
par Ericovitchi » 19 Oct 2010, 14:15
le -1 provient du -un
et tu ne sais pas réduire n/2(n+1) - 1 au même dénominateur ?
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 14:23
par alex-blade2 » 19 Oct 2010, 14:23
D'accord, mais alors le -1 n'est plus dans la 2ème étape alors ce qui donne :
} - 1 )u_n + \frac{3(n+2)}{2(n+1)} = (\frac{n-2n-2}{2(n+1)})u_n + \frac{3(n+2)}{2(n+1)}=(-\frac{n+2}{2(n+1)})u_n + \frac{3(n+2)}{2(n+1)}=\frac{(n+2)}{2(n+1)}(3-u_n))
Et pour passer de l'avant dernière à la dernière étape, quel procédé est utilisé ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Oct 2010, 14:31
par Ericovitchi » 19 Oct 2010, 14:31
j'ai mis (n+2)/(2(n+1)) en facteur
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 14:38
par alex-blade2 » 19 Oct 2010, 14:38
Ah oui, c'est bon.
J'ai une autre question il m'est dit :
On considère la suite (Vn) définie sur N* par :
)
Il faut prouver que cette suite est géométrique et préciser sa raison, mais quand je fais :

je ne trouve pas de constante, aurais tu un conseil ?
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 15:15
par alex-blade2 » 19 Oct 2010, 15:15
J'ai trouvé que
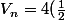^{n-1})
comment je peux exprimer

en fonction de n ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Oct 2010, 15:39
par Ericovitchi » 19 Oct 2010, 15:39
si Vn=n(3-Un) et que tu as trouvé Vn tu devrais pouvoir en déduire Un
-
alex-blade2
- Membre Naturel
- Messages: 74
- Enregistré le: 09 Avr 2009, 15:31
-
 par alex-blade2 » 19 Oct 2010, 15:47
par alex-blade2 » 19 Oct 2010, 15:47
Et bien justement j'arrive pas a en déduire Un

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Oct 2010, 16:04
par Ericovitchi » 19 Oct 2010, 16:04
une équation du premier degré !
Vn=n(3-Un) --> Vn/n=3-Un --> Un=3 - Vn/ n
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
