Inversion
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 29 Sep 2010, 17:19
par Reynolds » 29 Sep 2010, 17:19
Bonjour j'ai quelque petites questions:
Soit I->

1) Déterminer l'image d'une droite passant par 0 privée de 0
Je trouve que sa correspond à a la meme droite, j'ai utilisé des rotations mais sa me semble faux car on me demande l'image d'un cercle et I°I(z)= Id, donc je pense que c'est un cercle
2) Déterminer l'image d'une droite ne passant pas par O
J'ai essayé avec des rotations et je ne trouve rien...
Enfaite j'ai du mal a aborder le problème, comment écrire une équation de droite dans le plan complexe et comment la transformer par l'inversion?
Merci d'avance
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 29 Sep 2010, 17:32
par benekire2 » 29 Sep 2010, 17:32
Salut , quelle est l'équation d'une droite passant par (0,0) ? y=kx , tu peut pas en déduire une caractérisation complexe de cette droite ? Ensuite il te suffit de "faire passer à la machine" et de regarder ce que cela te donne.
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 29 Sep 2010, 17:58
par Reynolds » 29 Sep 2010, 17:58
Oai, mais je tombe alors sur un truc genre:
x'-
^2})
= 0
y'-
^2})
=0
Sa se rapproche d'une équation de cercle mais sa n'en ai pas une malheureusement.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Sep 2010, 18:06
par Doraki » 29 Sep 2010, 18:06
une équation de droite dans les complexes c'est une équation comme

avec a,b,c complexes.
Pour transformer ça en une équation de l'image par f du truc,
comme f(f(z)) = z, il suffit de remplacer z par f(z) :
z est dans f(D) f(z) est dans D f(z) vérifie l'équation de D.
Ensuite, pour voir que c'est léquation d'un cercle, il faut mettre en évidence que c'est sous la forme
\bar{(z-a)} + b = 0)
avec a complexe et b réel < 0.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 29 Sep 2010, 18:08
par Pythales » 29 Sep 2010, 18:08

est équivalent à

-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 29 Sep 2010, 19:23
par Reynolds » 29 Sep 2010, 19:23
Doraki je ne comprends pas vraiment t'as méthode, je trouve
Si z appartient a une droite privée de O, alors c nul
je trouve (za+bar(z))/zbar(z) (Désole c'est un mac je sais pas comment faire l'antislash)
Moi j'avais essayé avec z= x+ikx avec k réel
mais je ne trouve rien de conclant...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Sep 2010, 19:39
par Doraki » 29 Sep 2010, 19:39
Reynolds a écrit:Si z appartient a une droite privée de O, alors c nul
je trouve (za+bar(z))/zbar(z) (Désole c'est un mac je sais pas comment faire l'antislash)
Dans ce cas, l'équation de D est de la forme

.
et donc l'équation de f(D) ou de
)
est

, donc en multipliant par
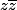
, tu as

, ce qui est l'équation initiale, donc on a bien que l'image d'une droite qui passe par 0 reste cette même droite.
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 29 Sep 2010, 19:45
par Reynolds » 29 Sep 2010, 19:45
Ok j'avais trouvé ce résultat en trouvant
})
=
)
avec une rotation basée sur le fait que la droite passe par 0 mais sa me semble louche,
Et pour la deuxième je mets un c alors?
Merci beaucoup
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Sep 2010, 19:47
par Doraki » 29 Sep 2010, 19:47
bah oui la deuxième c'est pareil sauf que tu as un c qui est non nul dans l'équation de D.
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 29 Sep 2010, 19:58
par Reynolds » 29 Sep 2010, 19:58
Je trouve rien, je ne sais pas isoler z et ma constante?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 29 Sep 2010, 20:03
par Pythales » 29 Sep 2010, 20:03
Mon message #5 montre que O,z et z' sont alignés...
Pour le 2, soit la droite
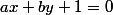
On pose

et

En remplaçant

par

et
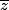
par

tu obtiens

soit un cercle passant par O, dont le centre est sur la ppd à la droite menée de O
(résultat bien connu de l'inversion)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Sep 2010, 20:39
par Doraki » 29 Sep 2010, 20:39
Ah excuse-moi, j'me suis gourré.
L'équation d'une droite c'est

, avec b réel.
Ce qui fait que après transformation, on trouve

, soit
\bar{(z+a/b)}-a\bar{a}/b = 0)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
