Déterminant non nul et inversion de matrice

[m.marc.m]

Bonjour à tous,

Quelles sont les différentes manières de démontrer que si A est une matrice à déterminant non nul alors elle est inversible?

Merci d'avance.
@+

[Deliantha]

La question à poser: quelles sont les différentes manières de montrer qu’une matrice est inversible ?
Une matrice d’ordre d’un corps ou anneau est inversible (ou régulière, voire non singulière)
s’il existe une matrice d’ordre telle que : alors 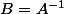l’inverse est unique.

Les propiétés suivantes sont équivalentes (en référer ici par ex. au § Matrice inversible de Wikipédia) :
• est inversible,
• est équivalente à la matrice unité d'ordre ,
• possède n pivots,
• le déterminant de est non nul : det,
• n'est pas valeur propre de ,
• le rang de est égal à ,
• le système homogène a pour unique solution,
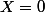• pour tout dans , le système linéaire a au plus une solution,
• pour tout dans , le système linéaire a au moins une solution,
• pour tout dans , le système linéaire a exactement une solution,
• les colonnes de , considérées comme des vecteurs de 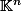, sont linéairement indépendantes,
• les colonnes de , considérées comme des vecteurs de 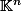, engendrent ,
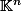• les colonnes de , considérées comme des vecteurs de 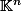, forment une base de ,
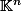• l'endomorphisme canoniquement associé à est injectif,
• l'endomorphisme canoniquement associé à est surjectif,
• l'endomorphisme canoniquement associé à est bijectif,
• la matrice est inversible à gauche, c-à-d qu'il existe une matrice carrée d'ordre n t.q. ,
• la matrice est inversible à droite, c-à-d qu'il existe une matrice carrée d'ordre n t.q. ,
• la transposée de est inversible,
• il existe un polynôme annulateur de dont n'est pas racine,
• n'est pas racine du polynôme minimal de .

[lartdeladivisionparzero]

Bonjour à tous,

Quelles sont les différentes manières de démontrer que si A est une matrice à déterminant non nul alors elle est inversible?

Merci d'avance.
@+

En partant du morphisme associé.
Soit u, endomorphisme d'un espace vectoriel E (de dimension n finie) dont on note B = (b1,...,bn) une base.
Alors u est un isomorphisme si et seulement si u(b1),...,u(bn) est une base de E donc si et seulement si detB(u(b1),...,u(bn)) est non nul (detB = déterminant dans la base B) donc si et seulement si det(u) est non nul.
Il faut en effet se rappeler que le déterminant est une forme n-linéaire alternée donc si (v1,...,vn) est libre dans E (comme c'est le cas pour une base), f(v1,...,vn) est non nul.

Ensuite tu te rapportes à la matrice de u et c'est bon