Bonjour, j'ai un QCM sur les suites avec différentes propositions, il faut dire si elles sont vrai ou fausses et les justifier. J'en ai réussi quelques unes, mais il y en a beaucoup que je ne sais pas justifier, pourriez vous m'aider pour les justification et me dire si celle que j'ai fait sont bonne ? les propositions sont :
1) Si (
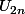
) et (
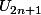
) sont convergentes, alors (

) est aussi convergente : j'ai mis faux, par exemple
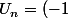^n)
2) Si (

) est convergente alors (
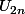
) et (
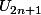
) est convergente aussi :
j'ai mis vrai mais je ne sais pas comment le justifier.
3) si
^2 = \alpha)
alors

+ ou -

J'ai mis que la proposition est vrai mais je ne sais pas le justifier j'ai éssayé en posant
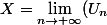 = 0)
mais je ne sais pas si cette méthode est bonne.
4) Si
 = 0)
, alors (

) est convergente
j'ai mis vrai, je ne sais pas justifier
5) Si (

) est convergente alors (

) est bornée : j'ai mis vrai mais je ne sais pas le justifier.
6) Peut on construire une suite (

) convergente, avec

=

+

telle que (

) ou (

) soit divergente
j'ai mis faux car je crois que le ou est exclusif (

) ou (

) car "soit" est au singulier. Mais je ne sais pas le justifier. Sinon si le ou n'est pas exclusif c'est vrai.
7) Peut on construire une suite (

) convergente avec

telle que (

) ou (

) soit divergente
j'ai mis vrai, par exemple

et
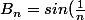)
8) Et sinon j'ai une autre question mais je trouve que ma réponse est peut être un peux simple :
Soient a et b deux réels vérifiant la proposition suivante :
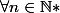

Que peut on affirmer ?
j'ai affirmé que
 = b = \lim_{n \to +\infty} (a+\frac{1}{n}))
, est ce tout ce que l'on peut dire ? ou ai-je oublié quelque chose ?
