Bonjour,
Je viens de finir ma dernière année dans le supérieur en professionnelle (équivalent à un bac pro en France).
Je vais continuer les études dans l'électromécanique, mais un problème survient.. Je n'ai jamais fait de math en dehors de calcul électrique et je dois absolument métissé la trigonométrie au plus vite.
C'est donc ici que je demande de l'aide, des sites me donnant les bases et des exercices ainsi que même des définition des mots telle que "cosinus sinus tangente".
//édit// J'aimerais aussi savoir comment faire quand on a un résultat au ² sur une calculette pour avoir l'inverse.. ex: 10² = 100 comment trouvé 10 si j'ai 100?
En vous remercient.
Max.
Lacune en trigonométrie
12 messages
- Page 1 sur 1
par lemax11 » 07 Sep 2010, 19:58
merci, mais j'ai déjà parcourue pas mal de site mais j'aurais aimé trouver un site avec un cour expliquant bien sans allé droit au exercice..
par lemax11 » 07 Sep 2010, 20:05
A merci beaucoups, et pour la question avec l'exposant?
Sa parle de la trigo sur les triangles rectangle?
Sa parle de la trigo sur les triangles rectangle?
par MacManus » 07 Sep 2010, 20:06
il faut taper 
, qui donne bien 10.
C'est le symbole "racine carrée".
C'est le symbole "racine carrée".
la trigo
par mathelot » 07 Sep 2010, 20:19
voiçi quelques principes de base
trigonométrie du triangle rectangle
Dans un triangle rectangle en A,
on distingue quatre quotients de longueurs de côtés
qui ne dépendent que de l'angle (de son écartement) et pas du triangle
on les nomme cosinus,sinus,tangente et cotangente de l'angle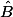
il y en a d'autres moins utilisés comme la sécante
ou la cosécante..
par exemple, dans un triangle pythagoricien de côtés 3,4,5
le sinus d'un des deux angles non droits vaudra vaudra
trigonométrie du cercle
On décide de généraliser le sinus et cosinus à des angles de mesure
plus que 90°
pour ce faire, on utilise les résultats suivants de géomètrie euclidienne
1) les angles de couple de vecteurs unitaires (de norme 1)
sont les rotations
2) les rotations sont des applications linéaires.
Notamment, elles conservent les figures que sont les parallélogrammes.
leurs "coordonnées" dans une base orthonormée, s'appellent matrices
on définit alors le cosinus "généralisé" d'un angle comme
la 1ère coordonnée de la matrice de rotation (rappelons que cette matrice de rotation est l'angle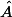
la 2ème coordonnée de la matrice de rotation s'appelle "sinus" (généralisé) de l'angle A.
3) il se produit alors un petit miracle, pour des angles inférieurs à 90°
les deux notions coïncident:
cosinus du triangle rectangle
cosinus de la rotation
voilà pour les nombres !
4) fonctions cosinus et fonction sinus
ensuite,il y a une fonction , construite à partir des nombres complexes,
qui vient enrouler la droite des nombres sur le cercle
la fonction "exponentielle complexe"
comment est-ce possible ?
Archimède, dès l'Antiquité , a sû mesurer les arcs de cercles
en les approchant par des lignes polygonales inscrites et exinscrites
ce procédé permet de parler de "longueur d'arc de cercle"
géoémtriquement , l'exponentielle complexe permet d'associer à un nombre
un point du cercle trigonométrique, obtenu en ayant
parcouru une longueur d'arc
Par correspondance bijective, les anglo-saxons disent "one-to-one mapping"
on associe à un réel, le point du cercle M(x) correspondant d'abscisse curviligne x, noté exp(ix),
puis l'angle)
que fait le vecteur 
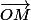
avec le 1er vecteur de base.
Tout ce passe bien, et à la somme de deux longueurs d'arc, va correspondre la composée successives des deux rotations
ce que l'on écrit succintement
}=e^{ia}.e^{ib})
cette notation étonnante , dûe à Léonhard Euler et étudiée par A.DeMoivre,
exprime que , à la somme de deux mesures d'arcs a+b,
correspond la composée de deux rotations, exprimée par le produit
de deux nombres complexes de module 1.
Ensuite , on passe aux coordonnées .
La 1re coordonnée, , le cosinus de la rotation , devient naturellement
cos(x) puisque cette rotation est paramétrée en quelque sorte par le réel x
Les mesures d'angles , modulo
sont des familles de mesures
du même angle, ,d'abscisse curviligne x, quand on ne distingue plus entre le nombre de tours effectués pour définir la rotation d'angle))
On dit alors que l'ensemble des mesures est "quotienté" par le modulo
derniers points
finalement, on construit ainsi deux fonctions réelles cos et sinus,
qui vont permettre d"'étudier n'importe quel phénomène périodique
c'est la théorie de Fourier
cette construction peut se retrouver, non pas avec le cercle,
mais avec d'autres courbes algébriques comme l'hyperbole
ou la lemniscate de Bernoulli.
Le principe est le même, le point courant sur la courbe
a pour coordonnées,sh(\phi)))
et le nombre qui paramètre le point de la courbe est interprété comme une mesure d'angle et ses coordonnées comme un cosinus et un sinus
5 ème point
il ya aussi des angles de droites. Ces angles ont à voir avec la "distance" entre deux droites. Il faut alors identifier les différents arcs de cercle
qui séparent ces deux droites et l'on obtient alors des mesures d'angles
modulo
et non pas
6ème point
localement, on remarque que les fonctions sinus et cosinus fournissent des applications bijectives.
on peut les inverser, on obtient les fonctions inverses arcsin,arccos et arctan
qui sont, rappelons le, des longueurs d'arcs
ces longueurs d'arc s'expriment au moyen de quadratures (d'intégrales)
exemples
=\int_{0}^{x} \, \frac{dt}{1+t^2})
=\int_{0}^{x} \, \frac{dt}{\sqrt{1-t^2}})
mathelot
trigonométrie du triangle rectangle
Dans un triangle rectangle en A,
on distingue quatre quotients de longueurs de côtés
qui ne dépendent que de l'angle (de son écartement) et pas du triangle
on les nomme cosinus,sinus,tangente et cotangente de l'angle
il y en a d'autres moins utilisés comme la sécante
ou la cosécante..
par exemple, dans un triangle pythagoricien de côtés 3,4,5
le sinus d'un des deux angles non droits vaudra vaudra
trigonométrie du cercle
On décide de généraliser le sinus et cosinus à des angles de mesure
plus que 90°
pour ce faire, on utilise les résultats suivants de géomètrie euclidienne
1) les angles de couple de vecteurs unitaires (de norme 1)
sont les rotations
2) les rotations sont des applications linéaires.
Notamment, elles conservent les figures que sont les parallélogrammes.
leurs "coordonnées" dans une base orthonormée, s'appellent matrices
on définit alors le cosinus "généralisé" d'un angle comme
la 1ère coordonnée de la matrice de rotation (rappelons que cette matrice de rotation est l'angle
la 2ème coordonnée de la matrice de rotation s'appelle "sinus" (généralisé) de l'angle A.
3) il se produit alors un petit miracle, pour des angles inférieurs à 90°
les deux notions coïncident:
cosinus du triangle rectangle
cosinus de la rotation
voilà pour les nombres !
4) fonctions cosinus et fonction sinus
ensuite,il y a une fonction , construite à partir des nombres complexes,
qui vient enrouler la droite des nombres sur le cercle
la fonction "exponentielle complexe"
comment est-ce possible ?
Archimède, dès l'Antiquité , a sû mesurer les arcs de cercles
en les approchant par des lignes polygonales inscrites et exinscrites
ce procédé permet de parler de "longueur d'arc de cercle"
géoémtriquement , l'exponentielle complexe permet d'associer à un nombre
parcouru une longueur d'arc
Par correspondance bijective, les anglo-saxons disent "one-to-one mapping"
on associe à un réel
puis l'angle
avec le 1er vecteur de base.
Tout ce passe bien, et à la somme de deux longueurs d'arc, va correspondre la composée successives des deux rotations
ce que l'on écrit succintement
cette notation étonnante , dûe à Léonhard Euler et étudiée par A.DeMoivre,
exprime que , à la somme de deux mesures d'arcs a+b,
correspond la composée de deux rotations, exprimée par le produit
de deux nombres complexes de module 1.
Ensuite , on passe aux coordonnées .
La 1re coordonnée, , le cosinus de la rotation , devient naturellement
cos(x) puisque cette rotation est paramétrée en quelque sorte par le réel x
Les mesures d'angles , modulo
du même angle, ,d'abscisse curviligne x, quand on ne distingue plus entre le nombre de tours effectués pour définir la rotation d'angle
On dit alors que l'ensemble des mesures est "quotienté" par le modulo
derniers points
finalement, on construit ainsi deux fonctions réelles cos et sinus,
qui vont permettre d"'étudier n'importe quel phénomène périodique
c'est la théorie de Fourier
cette construction peut se retrouver, non pas avec le cercle,
mais avec d'autres courbes algébriques comme l'hyperbole
ou la lemniscate de Bernoulli.
Le principe est le même, le point courant sur la courbe
a pour coordonnées
et le nombre qui paramètre le point de la courbe est interprété comme une mesure d'angle et ses coordonnées comme un cosinus et un sinus
5 ème point
il ya aussi des angles de droites. Ces angles ont à voir avec la "distance" entre deux droites. Il faut alors identifier les différents arcs de cercle
qui séparent ces deux droites et l'on obtient alors des mesures d'angles
modulo
6ème point
localement, on remarque que les fonctions sinus et cosinus fournissent des applications bijectives.
on peut les inverser, on obtient les fonctions inverses arcsin,arccos et arctan
qui sont, rappelons le, des longueurs d'arcs
ces longueurs d'arc s'expriment au moyen de quadratures (d'intégrales)
exemples
mathelot
un peu de glose pour conclure
par mathelot » 07 Sep 2010, 20:58
Si l'on démêle , de manière non formalisée, le véritable plat de spaguettis
que constitue l'exposé des mathématiques,
la trigonométrie vient de l'exponentielle complexe
qui vient des isométries
qui viennent du produit scalaire
qui vient du théorème de Pythagore
qui vient de la formule d'aire des triangles
qui vient de la formule d'aire des rectangles
qui vient de la multiplication de deux nombres..
que constitue l'exposé des mathématiques,
la trigonométrie vient de l'exponentielle complexe
qui vient des isométries
qui viennent du produit scalaire
qui vient du théorème de Pythagore
qui vient de la formule d'aire des triangles
qui vient de la formule d'aire des rectangles
qui vient de la multiplication de deux nombres..
par lemax11 » 07 Sep 2010, 21:03
Tout ça éclaircie l'esprit, j'ai été ce matin a un cours de remise a niv de math (niv supérieur) sans jamais avoir fait de la trigo et je commence désormais a calculé l'hypoténuse avec un cos et un angle adjacent.
Merci encore.
Merci encore.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :