Pb trigonométrie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 13:30
par grymist » 07 Sep 2010, 13:30
Bonjour, à tous les utilisateurs de se forum, je viens de ES, et dans ma prépa cette année je dois rattraper mon retard par rapport aux S.
Nous avon scommencé par la trigonométrie et j'ai bien peur de ne pas avoir tout compris. Il y a d'ailleur un exercice qui me bloque.
je dois montrer que l'expression est constante :
Cos^4x - sin^4x + 2sin²x
rien que le terme constante dans l'intitulé de l'exercice me bloque , que dois je trouver ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Sep 2010, 13:35
par girdav » 07 Sep 2010, 13:35
Bonjour,
tu peux t'aider de

valable pour tout réel

. Tu dois trouver un truc qui ne dépend pas de

.
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 13:42
par grymist » 07 Sep 2010, 13:42
c'est la seul formule dont j'ai besoin ?
si je fait
(cos²x)² - (sin²x)² + 2sin²x
est ce le bon debut ?
enfait je n'arrive pas à arriver à quelquechose qui ressemble à cos²x + sin²x .
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Sep 2010, 13:45
par girdav » 07 Sep 2010, 13:45
Exprime
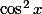
en fonction de

.
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 13:55
par grymist » 07 Sep 2010, 13:55
quelle est la formule ? j'ai beau chercher je ne trouve pas enfaite ...
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 14:00
par grymist » 07 Sep 2010, 14:00
(cos²x)² - (sin²x)² + 2sin²x
= (cos² - sin²x )² - (sin²x)² +2sin²x
= ((1-sin²x)-sin²x)² - ( sin²x)² +2 sin²x
Bien partit ou pas ?
( 1 -2sin²x)² -(sin²x)² + 2 sin²x
une fois la je vois pas trop , mais je voudrait savoir si c'est la bonne suite ?
-
romi64
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Sep 2010, 13:50
-
 par romi64 » 07 Sep 2010, 14:17
par romi64 » 07 Sep 2010, 14:17
Oupla non tu t'es trompé
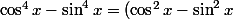(\cos^{2}x + \sin^{2}x))
=

et donc que se passe t-il ensuite ?
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 14:19
par grymist » 07 Sep 2010, 14:19
j'ai trouvé la reponse en faisant
(cos²x + sin²x )(cos²x - sin²x)+2sin²x
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 14:20
par grymist » 07 Sep 2010, 14:20
sa me fait cos²x -sin²x +2sin²x
= cos²x +sin²x
=1
la constante est donc 1 ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Sep 2010, 14:37
par girdav » 07 Sep 2010, 14:37
C'est ça. Une seul formule est intervenue donc.
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 14:46
par grymist » 07 Sep 2010, 14:46
Merci bien
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 15:41
par grymist » 07 Sep 2010, 15:41
j'ai une autre question ... ( je sui svraiment pas doué en trigo )
je devais exprimer cos3x*cosx en fonction de cos^4x et cos²x
soit :
j'en arrive à
(2cos^3x - cosx -( 2sinx * cosx) *sinx ) * cosx
j'aimerai sbien faire disparaitre les sinx , comment faire ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Sep 2010, 16:03
par girdav » 07 Sep 2010, 16:03
Tu peux dans un premier temps exprimer
)
en fonction de

et
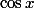
en te servant de
 =2\sin x \cos x)
.
-
Black Jack
 par Black Jack » 07 Sep 2010, 16:07
par Black Jack » 07 Sep 2010, 16:07
grymist a écrit:j'ai une autre question ... ( je sui svraiment pas doué en trigo )
je devais exprimer cos3x*cosx en fonction de cos^4x et cos²x
soit :
j'en arrive à
(2cos^3x - cosx -( 2sinx * cosx) *sinx ) * cosx
j'aimerai sbien faire disparaitre les sinx , comment faire ?
T'as fait le plus dur, il suffit de remarquer que :
( 2sinx * cosx) *sinx = 2sin²(x).cos(x) = 2.(1-cos²(x)).cos(x)
Et les sinus sont virés.
:zen:
-
grymist
- Membre Naturel
- Messages: 23
- Enregistré le: 07 Sep 2010, 13:26
-
 par grymist » 07 Sep 2010, 16:43
par grymist » 07 Sep 2010, 16:43
a voila !, c'est ce que je n'arrivait pas à faire, aprés tout devient logique , je vous remercie.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
