Bonjour,
Une fonction peut-elle être continue en un point qui n'appartient pas à son ensemble de définition ? (désolé, lacune...)
Merci.
Continuité
10 messages
- Page 1 sur 1
Salut,
Tu peut toujours la prolonger par continuité si tu le souhaite lorsque c'est possible.
Après par définition une application f:I-->J est continue en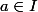 lorsque f(x)-f(a) tend vers 0 quand x tend vers a. Cela dit le f(a) implique que f soit définie ... ( et même le
lorsque f(x)-f(a) tend vers 0 quand x tend vers a. Cela dit le f(a) implique que f soit définie ... ( et même le 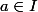 )
)
Donc non , une fonction ne peut être continue en un point où elle n'est pas définie.
Tu peut toujours la prolonger par continuité si tu le souhaite lorsque c'est possible.
Après par définition une application f:I-->J est continue en
Donc non , une fonction ne peut être continue en un point où elle n'est pas définie.
oui, c'est bien la définition.
f est continue en x0 si x0 appartient à l'ensemble de définition et = f(x_0))
Tu parlais d cas où x0 n'est pas dans l'ensemble de définition. Dans ce cas, on ne peut pas parler de continuité, mais éventuellement de prolongement par continuuité comme dans l'exemple que je t'ai donné.
f est continue en x0 si x0 appartient à l'ensemble de définition et
Tu parlais d cas où x0 n'est pas dans l'ensemble de définition. Dans ce cas, on ne peut pas parler de continuité, mais éventuellement de prolongement par continuuité comme dans l'exemple que je t'ai donné.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
