Equations différentielles

[VinS896]

Bonjour je bloque sur cette exercice.
On considère l'équation différentielle y' = -y
Soit f la solution de l'équation différentielle vérifiant f(0)=2
Calculer une valeur approchée au centième près par défaut de f(1):
f(1) =
Je vous remercie pour votre aide.

[Nightmare]

Salut,

surement as-tu déjà vue la méthode d'Euler qui est basée sur l'approximation affine : y'(0+h)=y(0)+hy'(0)+un reste.

[VinS896]

Je connais du nom mais jamais étudié, je la consulte en ce moment même pour essayer de la comprendre et trouver une solution.

[VinS896]

J'ai du mal à comprendre cette méthode.J'appelle au secours.

[Ericovitchi]

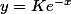
sinon tu trouves la solution de l'équation (y'=-y c'est dy/y=-dx donc en intégrant) ; Celle qui passe par (0,2) c'est et donc f(1)=2/e
et comme e~2.71828182845904523536 tu devrais pouvoir trouver facilement une valeur de 2/e

[VinS896]

Merci pour ta réponse. Je confirme tu as vu juste.