Edp

[egan]

Bonjour tout le monde,
J'aurais besoin de votre aide pour résoudre cette équation aux dérivées partielles.
Soit une fonction de dans vérifiant:

Déterminer .
J'ai essayé de trouver une fonction bijective de dans telle que les choses suivantes soient égales à quelque chose de sympathique:
-
-
-

Aucune de ces tentatives successives n'ont abouties. Je n'ai plus trop d'idée.
Du coup, je m'en remets à vous.
Merci d'avance.
@+ Boris.

[kazeriahm]

Salut,

g:(x,y)->x^2/2 est une solution particuliere, les solutions generales sont donc de la forme f=g+h ou h est une fonction harmonique sur R^2 (et ca il y en a un paquet)

[Finrod]

Salut,

g:(x,y)->x^2/2 est une solution particuliere, les solutions generales sont donc de la forme f=g+h ou h est une fonction harmonique sur R^2 (et ca il y en a un paquet)

J'ai comme un doute. Ce sont des dérivées seconde, donc il faudrait prendre mais marche aussi ...

Bon après l'esp des solutions sans second membre est bien un ev.

[kazeriahm]

oui of course autant pour moi pour le coup du x^3/6

evidemment il y en a un tas d'autre (d'ailleurs tu devais penser a xy^3/6 non ?) mais anyway si g est une solution particuliere alors f est solution si et seulement si f-g est harmonique donc l'ensemble des solutions f obtenues ne depend pas de la solution particuliere g choisie (puisqu'on a tout)

[kazeriahm]

oui of course autant pour moi pour le coup du x^3/6

evidemment il y en a un tas d'autre (d'ailleurs tu devais penser a xy^3/6 non ?) mais anyway si g est une solution particuliere alors f est solution si et seulement si f-g est harmonique donc l'ensemble des solutions f obtenues ne depend pas de la solution particuliere g choisie (puisqu'on a tout)

[Finrod]

euh non la dérivé seconde de xy²/2 par rapport à y est bien x.

, ça donne xy.

[egan]

Je n'ai pas tout suivi. Qu'est-ce qu'est une fonction harmonique?
Je ne connais pas du tout la théorie sur les edp, je cherche juste à savoir comment faire la résolution.

[Finrod]

http://fr.wikipedia.org/wiki/Fonction_harmonique

c'est un vaste sujet.

Il n'existe pas de résolution au sens où tu l'entends. Honnêtement, j'ignore jusqu'à quel point on sait décrire ces fonctions sur .


Par contre, c'est un espace vectoriel. Et l'ensemble des solutions de ton équation est un espace affine de direction cet espace vectoriel.

Sais-tu ce qu'est un espace vectoriel ?

Si non, connais tu la théorie que permet de résoudre une équa diff en prenant une solutions particulière + solution générale sans second membre ?

[egan]

Merci pour ta réponse.
Oui oui c'est bon je sais ce que sont les espaces vectoriels et affines.

[kazeriahm]

oui oui autant pour moi Finrod je dis vraiment nawak

bon sur R les fonctions harmoniques on les connait plutot bien (fonctions affines)

en dimension >1 elles verifient de super proprietes (C infini, principe du maximum et compagnie) mais elles forment un ev de dimension infinie

[Finrod]

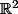
Je disais , je pensais tout à l'heure.

Comme tu parles de dimension, je suppose que c'est vrai pour tout .

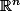
[Mathreach]

Pour moi tu doit utiliser les transformations de Fourier et il te faut en plus des condition initiales pour déterminer explicitement la fonction f.

[egan]

Comment tu utilises Laplace sur des fonctions à deux variables ?

[Mathreach]

Pour moi tu doit utiliser les transformations de Laplace et il te faut en plus des condition initiales pour déterminer explicitement la fonction f

[Mathreach]

On fait les transformations en sinus et en cosinus, et puis avec les conditions initiales on choisit la transformation adéquate.

[egan]

Je ne comprends pas trop ce que tu veux faire, tu peux me montrer sur un exemple stp ?