Billes blanches / noires, probabilités

[havemercy]

Bonjour,

Je réfléchis à une question de probabilité et je ne trouve malheureusement pas la réponse.

Voici la question :

Dans un grand panier, il y a 1'300 billes. Les billes sont blanches et noires. Il y a plus de billes noires que de blanches. En fait, il y a 98 % de billes noires et 2 % de billes blanches.

De ce grand panier, un hommes avec un bandeau sur les yeux tire 35 billes, que l'on place une à une dans un petit panier. Dans ces 35 billes, l'on trouve qu'il y a 70% de billes noires et 30 % de billes blanches.

la question est la suivante :

Le bandeau avait-il des trous ? OU plutot, combien y a-t-il de chances sur 100'000 pour que l'on se trouve avec une telle augmentation de billes blanches parmi les noires.

Merci pour vos aides.

Je recherche en particulier les formules ou théorèmes qui permettent de poser la solution.

[Finrod]

Dans ces 35 billes, l'on trouve qu'il y a 70% de billes noires et 30 % de billes blanches

Je sais pas si le bandeau avait des trous, mais le type a du faire son tirage au sabre, car il a tiré 10,5 biles blanches.

Sinon, sabre mis à part, il faut faire un test statistique qui permettra de mettre en évidence ce qui est déjà évident intuitivement, c'est à dire que la proba qu'il ai fait ça sans tricher est très très très très très très faible.

[havemercy]

Merci. Et un test de probabilité, cela se présente comment ?

[Finrod]

Dans ce cas là, le test de base est stupide.

Tu calcules la proba de parvenir au même résultat sans tricher et tu compares à un seuil fixé arbitrairement (En général 5, 2,5 ou 1 %).

Je dis que c'est stupide car on va forcement conclure qu'il a tricher. Les stats, sur une seule expérience, c'est jamais bien top.


Mais ça me rappelle un autre truc. Si tu calcules la proba de réussir sans tricher, il y a une formule pas bien compliqué pour calculer la proba de ne pas avoir triché sachant qu'il a réussi.

En gros passer de P(A sachant B) à P(B sachant A).

[Finrod]

Si p est la proba de réussir sans tricher. La proba de ne pas avoir triché sachant qu'on a réussi est

Donc c'est pô beaucoup.

[havemercy]

Aie, je me suis perdu en chemin, disons, juste après le premier tournant :we:

[Finrod]

A= Il a tiré exactement 30% de blanches sur 35 billes.
B= Il n'a pas triché
P(A/B): notation pour la proba de A sachant B
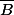: notation pour l'évènement complémentaire.
On pars de la formule

On a



Bon après il faut une hypothèse supplémentaire. Pour connaitre P(B). J'avais supposé qu'il n'y a aucune raison qu'il triche pluto qu'il ne triche pas à priori donc qui donne la formule du message précédant.

En toute généralité, on trouve un résultat qui dépend de P(B) et de P(A/B) :

[havemercy]

Merci beaucoup. J'ai aussi trouvé un site de calcul qui montre que la probabilité d'obtenir ce résultat est nulle ou très proche de 1 sur un milliard.