Bonjour,
Ceci n'est pas vraiment une énigme (mais pour moi, si !), j'ai 34 ans et je m'aperçois que j'ai oublié pas mal de choses en maths, j'espère que vous pourrez m'aider, c'est au sujet d'un jeu de jardinage en ligne...
Voici mon problème :
Une plante met un certain temps à pousser, disons "T" qui peut aller de 5 minutes à 336 H suivant la variété qu'on veut cultiver.
Il faut arroser les plantes toutes les 24 H
Il est possible dans ce jeu de développer du fertilisant au centre de recherche qui diminue de x% le temps de pousse restant à chaque arrosage.
Par exemple :
Pour cultiver des prunes, avec un fertilisant -16%, je suis arrivé à la conclusion que le temps de pousse initial donné de 10 jours (14400 minutes) était ramené à 7860 minutes (mais j'ai des arrondis au milieu, donc mon calcul n'est peut être pas très juste)...
Voici donc ma question :
Quelle formule permettrait de connaître le temps final de pousse d'une variété en fonction du temps de pousse initial et du niveau de fertilisant ?
Merci à vous qui me lirez
Bonjour à tous
5 messages
- Page 1 sur 1
salut,
je pige pas comment tu obtiens 7860.
Sinon, a partir de l'énoncé :
on note t_0 le temps de pousse initial.
Apres passage d'un coup de fertilisant, il vient
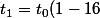 = t_0 \frac{21}{25} = 12096)
ou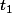 représente le temps de pousse si on a passé un seul coup de fertilisant.
représente le temps de pousse si on a passé un seul coup de fertilisant.
Après n+1 coups de fertilisants, on a
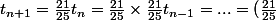^{n+1} t_0)
enfin, en supposant que tu passes tous tes coups de fertilisants le même jour lol
je pige pas comment tu obtiens 7860.
Sinon, a partir de l'énoncé :
on note t_0 le temps de pousse initial.
Apres passage d'un coup de fertilisant, il vient
ou
Après n+1 coups de fertilisants, on a
enfin, en supposant que tu passes tous tes coups de fertilisants le même jour lol
la vie est une fête 
Alors, pour obtenir 7860, je me suis fait une simulation sous excel :
temps total annoncé en plantant mes prunes :
14 400 minutes
1er arrosage à 16% : 12 096 minutes restantes annoncées
24 H plus tard
2nd arrosage : 8 951 minutes restantes annoncées (12 096 - 24 x 60) x (1-0,16)
24 H plus tard
3ème arrosage : 6 309 minutes restantes annoncées (8 951 - 24 x 60) x (1-0,16)
24 H plus tard
4ème arrosage : 4090 minutes restantes annoncées (6 309 - 24 x 60) x (1-0,16)
24 H plus tard
5ème arrosage : 2 226 minutes restantes annoncées (4 090 - 24 x 60) x (1-0,16)
24 H plus tard
6ème arrosage : 660 minutes restantes (moins de 24 H, donc mes prunes seront prêtes avant d'avoir à faire un septième arrosage) (2 226 - 24 x 60) x (1-0,16)
j'ai donc mon temps réel qui correspond à 660 minutes + 5 périodes de 24 H (1 440 minutes) soit 5 x 1 440 + 660 = 7 860 minutes
merci pour ta réponse fatal_error, je cherche la formule qui permet en connaissant la période (24H) et le pourcentage du fertilisant (qu'on peut améliorer dans le jeu), de trouver le temps réel de pousse à partir du temps initial.
Bonne soirée
temps total annoncé en plantant mes prunes :
14 400 minutes
1er arrosage à 16% : 12 096 minutes restantes annoncées
24 H plus tard
2nd arrosage : 8 951 minutes restantes annoncées (12 096 - 24 x 60) x (1-0,16)
24 H plus tard
3ème arrosage : 6 309 minutes restantes annoncées (8 951 - 24 x 60) x (1-0,16)
24 H plus tard
4ème arrosage : 4090 minutes restantes annoncées (6 309 - 24 x 60) x (1-0,16)
24 H plus tard
5ème arrosage : 2 226 minutes restantes annoncées (4 090 - 24 x 60) x (1-0,16)
24 H plus tard
6ème arrosage : 660 minutes restantes (moins de 24 H, donc mes prunes seront prêtes avant d'avoir à faire un septième arrosage) (2 226 - 24 x 60) x (1-0,16)
j'ai donc mon temps réel qui correspond à 660 minutes + 5 périodes de 24 H (1 440 minutes) soit 5 x 1 440 + 660 = 7 860 minutes
merci pour ta réponse fatal_error, je cherche la formule qui permet en connaissant la période (24H) et le pourcentage du fertilisant (qu'on peut améliorer dans le jeu), de trouver le temps réel de pousse à partir du temps initial.
Bonne soirée
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
