bonsoir :happy2:
je n'arrive pas à monter que y^2+z^2=(3-x^2)(x^2-2) n'admet pas de solution dans Q^3 à l'aide de la loi de réciprocité quadratique :S
Pouvez vous m'aider ?
merci d'avance
Loi de réciprocité quadratique :-)
4 messages
- Page 1 sur 1
Salut,
Je pense avoir une solution, mais c'est pas totalement trivial...
Si on prend irréductible, et
irréductible, et  ,
,  (pas forcément irréductibles), l'équation
(pas forcément irréductibles), l'équation
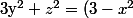(x^2-2)) dans
dans  devient
devient
=e^2(3b^2-a^2)(a^2-2b^2)) dans
dans  (ou
(ou  , c'est pareil ici)
, c'est pareil ici)
Or, le carré de tout entier est congru à 0 ou 1 modulo 4 et, comme et
et 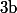 ne peuvent pas être pairs tout les deux, on n'a que 3 cas possibles pour
ne peuvent pas être pairs tout les deux, on n'a que 3 cas possibles pour  et
et  modulo 4 :
modulo 4 :

Ce qui montre qu'un des deux entiers et
et  est congru à 3 modulo 4.
est congru à 3 modulo 4.
La décomposition en nombre premier de cet entier contient donc un nombre premier congru à 3 modulo 4 qui apparait à une puissance impaire (preuve par l'absurde).
congru à 3 modulo 4 qui apparait à une puissance impaire (preuve par l'absurde).
Ce nombre premier ne peut pas apparaitre dans la décomposition de l'autre entier, car, si divisait à la fois
divisait à la fois  et
et  , il diviserait la somme
, il diviserait la somme  donc aussi
donc aussi  ce qui est absurde vu qu'on est parti avec
ce qui est absurde vu qu'on est parti avec =1)
Ce nombre premier (congru à 3 modulo 4) apparait donc à une puissance impaire dans
(congru à 3 modulo 4) apparait donc à une puissance impaire dans (a^2-2b^2)) donc aussi dans
donc aussi dans =e^2(3b^2-a^2)(a^2-2b^2)) donc aussi dans
donc aussi dans  .
.
Si on écrit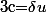 et
et 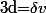 où
où 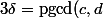) (donc
(donc =1) ), on a
), on a 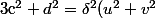) donc, de nouveau, le nombre premier
donc, de nouveau, le nombre premier  apparait à une puissance impaire dans
apparait à une puissance impaire dans  .
.
Cela signifie que c'est à dire que
c'est à dire que  .
.
Or, comme=1) , l'un (au moins) des deux est non nul modulo
, l'un (au moins) des deux est non nul modulo  donc en fait les deux sont non nuls modulo
donc en fait les deux sont non nuls modulo  et on a
et on a ^2\equ -1\ [p]) ce qui est absurde vu que
ce qui est absurde vu que  est congru à 3 modulo 4 et que l'on sait que -1 n'est un carré modulo
est congru à 3 modulo 4 et que l'on sait que -1 n'est un carré modulo  (impair) que lorsque
(impair) que lorsque  est congru à 1 modulo 4.
est congru à 1 modulo 4.
P.S. Si tu connait le théorème de ??? qui dit qu'un entier n est somme de deux carrés ssi les nombres premier congrus à 3 modulo 4 apparaissent à une puissance paire dans la décomposition de n, tu peut nettement abréger la preuve...
Je pense avoir une solution, mais c'est pas totalement trivial...
Si on prend
Or, le carré de tout entier est congru à 0 ou 1 modulo 4 et, comme
Ce qui montre qu'un des deux entiers
La décomposition en nombre premier de cet entier contient donc un nombre premier
Ce nombre premier ne peut pas apparaitre dans la décomposition de l'autre entier, car, si
Ce nombre premier
Si on écrit
Cela signifie que
Or, comme
P.S. Si tu connait le théorème de ??? qui dit qu'un entier n est somme de deux carrés ssi les nombres premier congrus à 3 modulo 4 apparaissent à une puissance paire dans la décomposition de n, tu peut nettement abréger la preuve...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ca, j'était sûr qu'y en aurait au moins un pour chercher.... :zen:
Sauf que ma propre recherche m'a conduit au nom :
"théorème de Fermat de Noël" (je déconne pas...)
du fait l'un des premier endroit où on trouve quasi complètement l'énoncé (avec des idées pour faire une preuve, mais pas la preuve elle même) est une missive de Pierre Fermat à Marin Mersenne datée du jour de Noël 1640.
En fait, la première trace qu'on a de l'énoncé complet est due à Albert Girard en 1634 (annotations sur la fin de la traduction commencée par Simon Stevin des livres de Diophante)
A noter aussi que :
"Le théorème sur les sommes de carrés figure aussi dans les fameuses observations que Fermat a écrit en marge de l'édition de Bachet des Arithmétiques de Diophante"...
Comme quoi, dans ces fameuse marge, ben y'avais pas mal de truc !!!
A noter enfin que Fermat finit par écrire qu'il a une "jolie preuve" du résultat (en utilisant la méthode dite de "descente infinie") mais que
"Aucune preuve rédigée par lui de ce théorème n'a subsisté"...
Enfin, il semblerait que la première preuve "répertoriée" du résultat soit dues à Leonhard Euler en colaboration avec Christian Goldbach...
Conclusion : le nom de "théorème de Lagrange" me... surprend...
Sauf que ma propre recherche m'a conduit au nom :
"théorème de Fermat de Noël" (je déconne pas...)
du fait l'un des premier endroit où on trouve quasi complètement l'énoncé (avec des idées pour faire une preuve, mais pas la preuve elle même) est une missive de Pierre Fermat à Marin Mersenne datée du jour de Noël 1640.
En fait, la première trace qu'on a de l'énoncé complet est due à Albert Girard en 1634 (annotations sur la fin de la traduction commencée par Simon Stevin des livres de Diophante)
A noter aussi que :
"Le théorème sur les sommes de carrés figure aussi dans les fameuses observations que Fermat a écrit en marge de l'édition de Bachet des Arithmétiques de Diophante"...
Comme quoi, dans ces fameuse marge, ben y'avais pas mal de truc !!!
A noter enfin que Fermat finit par écrire qu'il a une "jolie preuve" du résultat (en utilisant la méthode dite de "descente infinie") mais que
"Aucune preuve rédigée par lui de ce théorème n'a subsisté"...
Enfin, il semblerait que la première preuve "répertoriée" du résultat soit dues à Leonhard Euler en colaboration avec Christian Goldbach...
Conclusion : le nom de "théorème de Lagrange" me... surprend...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
