Gros probléme exercice
16 messages
- Page 1 sur 1
gros probléme exercice
salut voila plusieurs heure que je cherche a repondre a un question mais je bloque
montrer que M=C°teta est uen geodesique si et seulement si teta=(alpha,beta)
verifie le systeme d'equations differentielles:
(alpha)''=alpha((beta)')²sin²a
alpha(beta)''=-2(beta)'(alpha)'
je sais que C:(alpha,beta) E R * [0,2PI] -> (alpha sin a , beta , alpha cos a)
voila j'ai essayer en passant alpha et beta en polaire mais je n'avance pas
je pense qu'il faut integré mais je ne vois pas comment
pourriez vous m'iader
merci d'avance
Carla
montrer que M=C°teta est uen geodesique si et seulement si teta=(alpha,beta)
verifie le systeme d'equations differentielles:
(alpha)''=alpha((beta)')²sin²a
alpha(beta)''=-2(beta)'(alpha)'
je sais que C:(alpha,beta) E R * [0,2PI] -> (alpha sin a , beta , alpha cos a)
voila j'ai essayer en passant alpha et beta en polaire mais je n'avance pas
je pense qu'il faut integré mais je ne vois pas comment
pourriez vous m'iader
merci d'avance
Carla
Bon, je comprend pas gras du tout à ta formulation...
Si je ne m'abuse, a est une constante fixée d'avance.
Tu as une fonction définie par
définie par =\big(\alpha sin(a) , \beta , \alpha cos (a)\big))
C'est donc la restriction d'une appliction linéaire et ton application paramétrise donc une surface qui est un morceaux de plan dans lequel les géodésiques sont évidement... les lignes droites...
c'est à dire ce sont les fonction,\beta(t)\big)) telle que
telle que ) et
et ) sont affines.
sont affines.
Résumé : si tu veut qu'on t'aide, il faudrait fournir un contexte un peu plus correct, par exemple donner clairement quelle est la surface (ou variétée) sur laquelle tu te place avant de parler de géodésiques !!!!
Si je ne m'abuse, a est une constante fixée d'avance.
Tu as une fonction
C'est donc la restriction d'une appliction linéaire et ton application paramétrise donc une surface qui est un morceaux de plan dans lequel les géodésiques sont évidement... les lignes droites...
c'est à dire ce sont les fonction
Résumé : si tu veut qu'on t'aide, il faudrait fournir un contexte un peu plus correct, par exemple donner clairement quelle est la surface (ou variétée) sur laquelle tu te place avant de parler de géodésiques !!!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ton "exercice" ne commence pas par "Soit S la surface....." ????
P.S. à mon avis, ta surface c'est l'image de ta fonction C, mais je pense que ce n'est pas celle que tu nous a donné : dans ce cas, l'exo n'aurait absolument aucun intérêt !!!!
Qui est 'a' dans ta formule ?
P.S. à mon avis, ta surface c'est l'image de ta fonction C, mais je pense que ce n'est pas celle que tu nous a donné : dans ce cas, l'exo n'aurait absolument aucun intérêt !!!!
Qui est 'a' dans ta formule ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si ta surface est un cône de révolution d'axe y'Oy, une paramétrisation possible est :
\mapsto\big(k\beta \cos(\alpha)\, ,\, \beta\, ,\, k\beta\sin(\alpha)\big)\) où
où 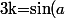)
Si par hasard c'est bien la paramétrisation du cône que l'on te donne (???) pour trouver les géodésiques, on cherche les fonction\,,\, \beta(t) \big)) telles que le vecteur accélération de la courbe paramétré
telles que le vecteur accélération de la courbe paramétré ,\beta(t)\big)) soit en tout point orthogonal à la surface.
soit en tout point orthogonal à la surface.
Si par hasard c'est bien la paramétrisation du cône que l'on te donne (???) pour trouver les géodésiques, on cherche les fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
alors la premiére question me demande en réalité de determiné la parametrisation et j'ai effectivement la meme chose que toi
j'ai mis tous de suite sin a je n'ai pas utilisé k
plus exactement x=Beta cos (alpha) sin(a)(
y=Beta
z=Beta sin(alpha) sin (a)
voila mais je ne comprend toujours pas le rapport avec le systeme d'equation
ps: je sais je ne suis pas doué en math , je suis physicien a la base
merci d'avance pour ton aide
carla
j'ai mis tous de suite sin a je n'ai pas utilisé k
plus exactement x=Beta cos (alpha) sin(a)(
y=Beta
z=Beta sin(alpha) sin (a)
voila mais je ne comprend toujours pas le rapport avec le systeme d'equation
ps: je sais je ne suis pas doué en math , je suis physicien a la base
merci d'avance pour ton aide
carla
Si tu est physicien, on risque d'avoir des problèmes de notations...
Si to a^N désigne l'accélération normale, ce n'est pas la bonne définition dans un cas comme celui là : ici une géodésique c'est une trajectoire telle que l'accélération normale soit orthogonale au plan tangent en tout point.
Si tu veut une visualisation concrète, lorsque tu roule "en ligne droite" à vitesse constante dans une region de collines, à chaque somme de cote et à chaque fond de vallée, ton accélération normale n'est pas nulle à cause de la courbure haut/bas de la route, par contre, elle est dirigé perpendiculairement par rapport au sol : le seul "virage" que tu fait est bas/haut et pas de virage droite/gauche : tu ne touche ni au volant, ni à l'accélérateur mais tu ne suit pas une droite de R^3 du fait que le sol n'est pas plat !
Au niveau calcul, tu doit determiner les deux vecteurs directeurs du plan tangent au "point courrant" C(alpha,beta) ainsi que l'accélération de la courbe paramétrée t->C(alpha(t),beta(t)) puis exprimer que l'accélération doit être perpendiculaire aux deux vecteurs directeurs à l'aide de produits scalaires.
Tu obtient alors deux équations.
Si to a^N désigne l'accélération normale, ce n'est pas la bonne définition dans un cas comme celui là : ici une géodésique c'est une trajectoire telle que l'accélération normale soit orthogonale au plan tangent en tout point.
Si tu veut une visualisation concrète, lorsque tu roule "en ligne droite" à vitesse constante dans une region de collines, à chaque somme de cote et à chaque fond de vallée, ton accélération normale n'est pas nulle à cause de la courbure haut/bas de la route, par contre, elle est dirigé perpendiculairement par rapport au sol : le seul "virage" que tu fait est bas/haut et pas de virage droite/gauche : tu ne touche ni au volant, ni à l'accélérateur mais tu ne suit pas une droite de R^3 du fait que le sol n'est pas plat !
Au niveau calcul, tu doit determiner les deux vecteurs directeurs du plan tangent au "point courrant" C(alpha,beta) ainsi que l'accélération de la courbe paramétrée t->C(alpha(t),beta(t)) puis exprimer que l'accélération doit être perpendiculaire aux deux vecteurs directeurs à l'aide de produits scalaires.
Tu obtient alors deux équations.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
c'est dans la cadre d'uncour de math donc niveau notation sa devrait aller
mais j'ai essayé de faire se que tu as ecrit à plusieurs reprise mais je ne tombe pas sur deux equations donc voila je ne sais pas trop comme m'y prendre
voila je ne vois vraiment plus comment faire
carla
ps: je ne suis pas blonde
mais j'ai essayé de faire se que tu as ecrit à plusieurs reprise mais je ne tombe pas sur deux equations donc voila je ne sais pas trop comme m'y prendre
voila je ne vois vraiment plus comment faire
carla
ps: je ne suis pas blonde
Si une paramétrisation de ta surface est :
\mapsto\big(k\beta \cos(\alpha)\, ,\, \beta\, ,\, k\beta\sin(\alpha)\big)\) où
où ) (j'avais écrit une connerie...)
(j'avais écrit une connerie...)
alors au point) , le plan tangent à la surface est dirigé par
, le plan tangent à la surface est dirigé par
\, ,\, 0\, ,\, k\beta\cos(\alpha)\big)\ =\ k\beta\big(-\sin(\alpha)\, ,\, 0\, ,\, \cos(\alpha)\big))
\, ,\, 1\, ,\, k\sin(\alpha)\big)\ =\ k\big(\cos(\alpha)\, ,\, \frac{1}{k}\, ,\, \sin(\alpha)\big)\)
Si on considère une courbe paramétrée par=C\big(\alpha(t),\beta(t)\big)) (donc par construction contenue dans la surface) alors :
(donc par construction contenue dans la surface) alors :
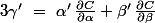 (évidement contenu dans le plan tangent !!)
(évidement contenu dans le plan tangent !!)
<br />+\beta^{\prime\prime}\frac{\partial C}{\partial\beta}<br />+\beta^\prime\big(\alpha^\prime\,\frac{\partial^2 C}{\partial\alpha\partial\beta}+\beta^\prime\, \frac{ \partial^2 C}{ \partial\beta^2 }\big))
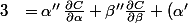^2\,\frac{\partial^2 C}{\partial\alpha^2}<br />+2\alpha^\prime\beta^\prime\,\frac{\partial^2 C}{\partial\alpha\partial\beta}<br />+(\beta^\prime)^2\, \frac{ \partial^2 C}{ \partial\beta^2 })
et il faut que le produit scalaire de avec
avec  et avec
et avec  soit nul.
soit nul.
Il faut donc évaluer les dérivées secondes ,
,  et
et  puis les produit scalaires :
puis les produit scalaires :

Je te laisse terminer...
alors au point
Si on considère une courbe paramétrée par
et il faut que le produit scalaire de
Il faut donc évaluer les dérivées secondes
Je te laisse terminer...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Il y a quand même un gros problème : si l'énoncé ne te donne pas la paramétrisation choisie du cône (il y en as des tas et des tas), je vois pas comment l'énoncé pourrait te donner les équations sur lesquelles tu doit tomber : elles dépendent évidement de la paramétrisation choisie !!!!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
bon, déjà on avance un peu, la paramétrisation n'est pas sensée être quelconque, mais orthogonale, ça limite un peu le choix.
Sauf qu'il continue à y avoir une infinité de paramétrisations orthogonales... (dont celle çi dessus) donc tu peut trouver quasiment ce que tu veut comme condition sur les fonctions alpha et beta en fonction de la paramétrisation choisie...
Bon, lit tout bien ton énoncé, tu est sûr qu'en plus d'être orthogonale ta paramétrisation n'est pas sensée avoir d'autres propriétés ?
Sauf qu'il continue à y avoir une infinité de paramétrisations orthogonales... (dont celle çi dessus) donc tu peut trouver quasiment ce que tu veut comme condition sur les fonctions alpha et beta en fonction de la paramétrisation choisie...
Bon, lit tout bien ton énoncé, tu est sûr qu'en plus d'être orthogonale ta paramétrisation n'est pas sensée avoir d'autres propriétés ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
