Règle d'intégration

[gabbbouch]

Je dois calculer l'intégrale suivante:

T(y)= y(1/1+y2), le 2 est un exposant

Dans le corrigé, ils ajoutent des 2 afin de calculer cette intégrale

T(y)= 1/2 2y(1/1+y2), le dernier 2 étant un exposant et la réponse finale est

T(y)= ln(1+y2) + C, la parenthèse est en fait une racine carrée.

Je ne comprends pas l'étape durant laquelle ils ajoutent des 2, est-ce une formule?

[ned aero]

salut,

T(y)= y(1/1+y²) = y/(1+y²)

pose u = 1+y² ==> u'= 2y donc y/(1+y²) = (1/2)*u'/u

la primitive de u'/u est ln|u| +C ==> la primitive de (1/2)*u'/u est (1/2)*ln|u| +C

soit (1/2)*ln|1+y²| +C = (1/2)*ln(1+y²)+C car 1+y²> 0

comme on sait que n*lna= ln (a^n)
..............................................................______
=> (1/2)*ln(1+y²)+C = ln[(1+y²)^1/2)+C= ln;)(1+y²)+C

[Teacher]

Illisible :)

[Mathusalem]

Je dois calculer l'intégrale suivante:

, le 2 est un exposant

Dans le corrigé, ils ajoutent des 2 afin de calculer cette intégrale

, le dernier 2 étant un exposant et la réponse finale est

, la parenthèse est en fait une racine carrée.

Je ne comprends pas l'étape durant laquelle ils ajoutent des 2, est-ce une formule?

Est-ce que comme ça c'est plus lisible ":)" ?

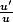
Toujours est-il qu'ils ne rajoutent pas des 2. Ils rajoutent un 2/2 (fois 1) qu'ils séparent en afin d'avoir la dérivée interne exacte de devant. Grâce à ceci, ils obtiennent une forme dont l'integrale est ln(u). Donc à la fin, je ne trouve pas une racine.

[gabbbouch]

Merci beaucoup je comprends maintenant que je pouvais procéder par changement de variable.

Mais comment puis-je faire pour calculer ;)(sec²;)x)/;)x, dans le corriger ils procède de la même facon en ajoutant 2/2 mais dans ce cas-ci je ne vois pas comment je pourrais faire un changement de variable..