[Reglé] Polynomes de degres superieur à 2 / Equations bicarr

[brickster]

Parfait, merci beaucoup ;)

Maintenant pour le 69, pourrait tu me dire comment on commence le 1) ? :doh:

[Rower]

tu pose x²=X
donc x^4-13x²+36=0
devient X²-13X+36=0
tu rèsout cette équation
et tu trouve X' et X''
or X=x²
donc on a X'=x² et X''=x²
;)x²=±;)X'
;)x²=±;)X''

on a donc 4 solutions
+;)X',-;)X',+;)X'',-;)X''

[brickster]

Merci, j'essaye tout de suite

[brickster]

Parfait, je trouve 2, -2, 3,-3

Pour le deuxieme, je fais exactement pareil ?

[brickster]

Justement pour la 2e équation, j'obtiens
X'=-4 et X''=-1

C'est donc impossible ?

[Rower]

et oui tout a fait
car x²;)0

[brickster]

OK, donc je met l'equation n'a pas de solution

[Rower]

Oui que l'equation n'a pas de solutions dans R(ensemble des nombres réels)

Enfin, je tiens à t'informer que ce n'est pas impossible
mais tu verras cela par la suite en année de terminale donc inutile de précipiter les choses

[brickster]

Ah oui, chaque chose en son temps !

Bon eh bien voila, j'ai reussi et surtout tout compris.

Merci à vous deux pour votre aide ;)

[Elsa_toup]

Juste une petite chose.
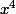
Tu as dit que tu trouvais quoi comme racines au final pour -9x²+4x+12 = 0 ????

Parce que j'ai comme l'impression qu'il y a un truc qui cloche ...

[Rower]

J'ai pas vérifié si son résultat était bon ... dèsolé

[Elsa_toup]

Pas de problème... :we:
C'est moi qui étais responsable du premier exo :lol4:

Mais en l'occurrence, il est faux je crois.
Le reste est bon, de ce que j'ai pu voir...

[brickster]

Ah !!
Peux tu me dire dans partie de l'exercie n'est pas bonne ?

bouhhh

[Elsa_toup]

Pour p(x)=0, je trouve

x1=9-65
----------
2

x2=9+65
----------
2

Ca c'est faux.
Réécris ton polynome ax²+bx+c, avec les valeurs exactes de a, b et c (que tu as trouvées).

Et recalcule delta.

Dis-moi ce que tu trouves....

[brickster]

Ah, je crois avoir compris, il fallait mettre x^4 de coté.
J'ai mal fait

[brickster]

Hum...je comprend plus bien.
Au 2), j'ai trouvé les valeur a, b et c

Pour le 3), je reprend ces valeur ou juste avec -9x²+4x+12 en mettant x^4 de coté ?
et la
a=-9
b=4
c=12

[Elsa_toup]

Tu as écrit:

Super, j'ai reussi
a=1
b=a=1
c=-6

C'était juste.

Donc maintenant (je suis toujours dans l'exercice 1), écris le polynôme P(x).
Tu dois avoir: P(x) = (x+1)(x-2)(ax²+bx+c).

Tu ne considères ensuite que ax²+bx+c et tu en trouves les racines.

[brickster]

Oui tu as raison, je viens de trouver Delta=25, et la tout est clair, à la fin
S={-3;2}

Par rapport au 4), j'ai changé aussi, mais je trouve deux fois x=2.

C'est grave docteur ?

[Elsa_toup]

lol, non mon petit, c'est un problème bénin...

En fait, on dit dans ce cas que 2 est "racine double", mais ton ensemble de solutions reste: S = {-3, -1, 2}.

En revanhe tu peux écrire P(x) = (x+3)(x+1)(x-2)²
Et là, c'est merveilleux !!! Non ? :doh:

[Rower]

c'est de la magie Elsa ^^